
Читайте также:
|
1. Комбинаторика
1.1. Сколько прямых можно провести через 8 точек, никакие 3 из которых не лежат на одной прямой, так чтобы каждая прямая проходила через 2 точки?
1.2. Сколькими способами можно расставить на полке 7 различных книг, чтобы определенные 3 книги: а) стояли рядом? б) не стояли рядом?
1.3. Найти m и n, если  .
.
1.4. Вычислить:  .
.
2. Случайные события.
2.1. Игральная кость бросается один раз. Найти вероятность того, что появится не менее трех очков.
2.2. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна пяти, а произведение – четырем.
2.3. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.
2.4. Пусть, испытание-приобретение одного лотерейного билета; событие А-«выигрыш 1000 рублей»; событие B – «любой выигрыш», событие C-«отсутствие выигрыша». Найти A+B+C, A·B·C, (A+B)·C, (A+C)·B. Как называются полученные события? Что можно сказать об их вероятностях? Объяснить полученные результаты.
3. Формула полной вероятности и формула Байеса.
3.1. В вычислительной лаборатории имеются 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
3.2. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму – 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым – 0,98. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что это изделие проверил второй товаровед.
4. Схема Бернулли повторения испытаний. Формула Бернулли, формула Лапласа.
4.1. Производится четыре независимых опыта, в каждом из которых событие А происходит с вероятностью 0,3. Событие В наступает с вероятностью, равной 1, если событие А произошло не менее двух раз; не может наступить, если событие А не имело места, и наступает с вероятностью 0,6, если событие А имело место один раз. Определить вероятность появления события В.
4.2. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найти наивероятнейшее число образцов, которые товаровед признает годным к продаже.
4.3. Рассчитать вероятность хотя бы одного появления события А при 10 независимых опытах от вероятности р появления события А в каждом опыте для р= 0,05.
4.4. Игра состоит в набрасывании колец на колышек. Игрок получает 6 колец и бросает кольца до первого попадания. Найти вероятность того, что хотя бы одно кольцо останется неизрасходованным, если вероятность попадания при каждом броске равна 0,1
5. Законы распределения и числовые характеристики дискретных случайных величин.
5.1. Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
5.2. Составить закон распределения разности независимых случайных величин Х1 и Х2, имеющих следующие законы распределения:
| Значение Х1 | |||
| Вероятность | 0,3 | 0,5 | 0,2 |
| Значение Х2 | -1 | |
| Вероятность | 0,4 | 0,6 |
5.3 В парке отдыха организована беспроигрышная лотерея. Имеется 1000 выигрышей, из них 400 – по 100 руб.; 300 – по 200 руб.; 200 – по 1000 руб. и 100 – по 2000 руб. Какой средний размер выигрыша для посетителя парка, купившего один билет?
5.4 Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной законом распределения:
| Значение Х | -5 | |||
| Вероятность | 0,4 | 0,3 | 0,1 | 0,2 |
5.5. Найти дисперсию дискретной случайной величины Х – числа появления события А в пяти независимых испытаниях, если вероятность появления события А в каждом испытании равна 0,2.
5.6. Найти центральные моменты первого, второго и третьего порядка, если случайная величина Х задана законом распределения:
| Значение Х | |||
| Вероятность | 0,1 | 0,3 | 0,6 |
6. Законы распределения и числовые характеристики непрерывных случайных величин.
6.1. Случайная величина Х задана интегральной функцией

Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0,25; 0,75).
6.2. Если график плотности распределения случайной величины Х имеет вид:
 , то D(4Х - 2) =
, то D(4Х - 2) =
6.3. Если случайная величина X задана плотностью распределения  то M(3X+2) равна…
то M(3X+2) равна…
6.4. Найти дисперсию случайной величины Х, заданной интегральной функцией

7. Случайные векторы и многомерные распределения.
7.1. Задано распределение вероятностей дискретной двумерной случайной величины
| Х | ||||
| Y | ||||
| 2,3 | 0,05 | 0,12 | 0,05 | 0,04 |
| 2,7 | 0,09 | 0,30 | 0,11 | 0,21 |
Найти законы распределения составляющих.
7.2. Задана интегральная функция двумерной случайной величины

Найти дифференциальную функцию системы.
7.3. Задана дискретная двумерная случайная величина
| Х | х1=2 | х2=5 | х3=8 |
| Y | |||
| у1=0,4 | 0,15 | 0,30 | 0,35 |
| у2=0,8 | 0,05 | 0,12 | 0,03 |
Найти: а) условный закон распределения составляющей Х, при условии, что составляющая Y приняла значение у1=0,4; б) условный закон распределения Y, при условии, что Х приняла значение х2=5.
7.4. Задана дифференциальная функция непрерывной двумерной случайной величины (Х,Y)

Найти математические ожидания составляющих Х и Y.
7.5. Задана дифференциальная функция непрерывной двумерной случайной величины (Х,Y):  в квадрате 0≤х≤π, 0≤у≤π; вне квадрата
в квадрате 0≤х≤π, 0≤у≤π; вне квадрата  . Найти корреляционный момент.
. Найти корреляционный момент.
8. Закон больших чисел. Центральная предельная теорема.
8.1. Случайные величины Х и У независимы и имеют равномерное распределение на отрезке [0,2]. Найти характеристическую функцию и математическое ожидание случайной величины Х+У.
8.2. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется меньше двух.
8.3. Последовательность независимых случайных величин Х1, Х2, …, Хn, …, задана законом распределения
| Хn | -nα | nα | |
| р | 1/n² | 1-1/n² | 1/2n² |
Применима ли к заданной последовательности теорема Чебышева?
9. Математическая статистика.
9.1. Интересуясь размером проданной в магазине мужской обуви, мы получили данные по 100 проданным парам обуви и нашли эмпирическую функцию распределения:

Сколько обуви 40-ого размера было продано?
9.2. Из текущей продукции автомата, обрабатывающего ролики диаметром 20 мм, взята выборка объемом 100 штук. Ролики измерены по диаметру микрометром с ценой деления 0,01мм. По данным отклонений от номинального размера диаметра построена гистограмма частот.

Сколько роликов имеют отклонение x от номинального размера диаметра, удовлетворяющее неравенству 0.04<x<0.08?
9.3. Результаты сдачи экзамена по Теории вероятностей группой из 10 студентов приведены в таблице:
| № студента по списку | ||||||||||
| Полученная оценка |
Чему равны средняя оценка, исправленная дисперсия, исправленный стандарт, размах, мода и медиана?
9.4. Студенты группу из 20 человек получили следующие оценки на экзамене по математике:
Составить частотный ряд, построить полигон и гистограмму, вычислить среднее, исправленную дисперсию, исправленный стандарт, медиану размах, моду.
9.5. Найти оценку для параметра λ распределения Пуассона, имеющего закон распределения
 ,
,
используя выборку, определяемую таблицей
| хi | |||||
| ni |
9.6. Двумя методами (методом моментов и методом наибольшего правдоподобия) найти оценку для параметра р распределения Бернулли, имеющего закон распределения
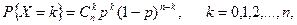
используя выборку, определяемую таблицей
| хi | |||||
| ni |
ЛИТЕРАТУРА
1.Ахтямов, А.М. "Теория вероятностей". - М.: Физматлит, 2009
2.Гмурман, В. Е. «Теория вероятностей и математическая статистика»: Учеб. пособие — 12-е изд., перераб.- М.: Высшее образование, 2010.-479 с.:ил (Основы наук).
3.Гмурман, В. Е. «Руководство к решению задач по теории вероятностей и математической статистике»: Учеб. пособие — 11-е изд., перераб. — М.: Высшее образование, 2010.-404 с. (Основы наук).
Вопросы обсуждены и одобрены на заседании кафедры «Общих математических и естественнонаучных дисциплин»
Протокол №1 от 31августа 2013года
Зав.кафедрой А.Ю.Байков
Дата добавления: 2015-02-16; просмотров: 309 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Нормальный закон распределения Гаусса для непрерывных величин | | | Классический метод задания вероятности. |