Читайте также:
|
Поле передает действие одного заряда на другой. Как оно изменится, если источник поля будет двигаться с высокой скоростью? Для гиперболизации предположим, что скорость релятивистская, V близка к скорости света.
В таком случае мы вправе использовать выводы специальной теории относительности Эйнштейна.
СТО предсказывает сокращение продольных размеров всех материальных тел. Но поле тоже материально. Следовательно, необходим учет перераспределения в "сокращенном" пространстве линий напряженности поля Е. Схематически это можно представить следующим рисунком
 Если изотропное поле неподвижного заряда обозначить как Е0, то напряженность в точке, расположенной под некоторым углом к направлению движения заряда, будет равна:
 Чтобы выделить различие между сравниваемыми полями, вычислим величину работы по какому либо замкнутому контуру в статическом поле и в поле движущегося заряда.
 При перемещениях по путям от точки 2 к точке 3 и от точки 4 к точке 1 вектор силы F= qE направлен перпендикулярно перемещению так, что в обоих полях работа на этих путях равна нулю.
При перемещениях по пути 1-2 направление вектора силы совпадает с направлением перемещения и работа положительна. Наоборот, на путях 3-4 работа отрицательна, так как вектор силы направлен против перемещения.
а) В изотропном поле неподвижного заряда величина напряженности Е одинакова для точек 2 и 3 или для 4 и 1, следовательно равны и значения силы в соответствующих точках. По модулю работа одинакова, что для перемещения 1-2, что для пути 4-1, знаки же разные. Полная работа для замкнутого контура в первом случае равна нулю. Говорят, что такое поле потенциально.
б) Другая ситуация для неизотропного поля движущегося заряда. Здесь в области 3-4 напряженность поля гораздо выше, чем в области 1-2. Это видно из различия в густоте линий Е на рисунке и строго математически следует предыдущей из формулы. По этой причине заметно различаются и силы, так что полная работа не может быть равна нулю. Поле движущегося заряда непотенциально!
| ||||||
И обладает дополнительными свойствами, отличающими его от статического поля. Естественно считать, что новые свойства являются проявлением какого то другого, дополнительного поля, которым обладает движущийся заряд. Это поле известно под названием магнитного, оно передает магнитное взаимодействие зарядов
|
| 10)Магнитное поле в веществе | |
При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки.Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками.Характеризует магнитное поле в веществе вектор  , равный геометрической сумме  и  магнитных полей:  Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность  , равная отношению магнитного момента малого объема вещества к величине этого объема:  где  – магнитный момент i -го атома из числа n атомов, в объеме Δ V Для того чтобы связать вектор намагниченности среды с током  , рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень длиной h и поперечным сечением S (рис. 6.3, а). Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала повсюду постоянна. Гипотеза Ампера. Ампер высказал предположение, что молекулярный магнетизм является следствием того, что в молекулах текут круговые, вечные электрические токи.По Амперу получалось, что, собственно говоря, магнетизм даже не существует как некое отдельное явление, что магнитное действие всегда вызывается электрическим током.Ампер высказал очень проницательное соображение" Современная физика установила, что магнитные свойства вещества определяются движением электрически заряженных частиц, из которых состоят атомы.Как мы знаем, в веществе в самом деле есть вечные токи, о существовании которых догадывался Ампер.Вращающийся вокруг атомного ядра электрон, несущий в себе отрицательный заряд, - ведь это и есть вечный электрический ток.Электрон вращается не только вокруг ядра, он вращается и вокруг своей оси, ведет себя подобно Земле, обращающейся вокруг Солнца. Вращение электрона вокруг своей оси также подобно электрическому току, также создает магнитное поле.Магнетизм железа и других ферромагнитных металлов-никеля, кобальта-и объясняется в основном как раз вращением электронов атомов вокруг своей оси.Гипотезы Вебера и Ампера, пытавшихся дать объяснение намагничению железа, давали только качественное объяснение этому явлению. Для количественных расчетов эти гипотезы, в то время недостаточно разработанные, не ставшие еще законами, конечно, не годились.Как именно происходит поворот молекулярных магнитиков под действием магнитного поля, как зависит способность железа намагничиваться от величины этого поля - оставалось неизвестным. Это было громадным пробелом в электротехнике.Создатели динамомашин и электромоторов уже издавна пользовались железом. Этот металл - сердцевина всех электрических машин. Недаром инженеры назвали сердечниками железные части моторов, электромагнитов, динамомашин. Но, то и дело применяя железо, электротехники работали кустарно, почти вслепую.Мало что было известно ученым о процессе намагничения железа, о том, через какие стадии проходит, намагничиваясь, железо, зависит ли, и если зависит, то как именно, способность железа "впитывать" магнетизм от силы магнитного поля, в котором оно находится, и от способности к намагничению различных сортов железа.Обматывая сердечники своих машин проволокой, электротехники руководствовались простым соображением: чем больше намотать витков, тем сильнее будет магнитное поле, создаваемое катушкой. А о железе, помогающем усиливать это поле, они и не думали. В выгодные или невыгодные условия будет поставлено железо, в надлежащем ли режиме придется работать сердечнику - мысль об этом в те времена никого не беспокоила. Не было у электротехников и критерия, которым можно было бы руководствоваться при выборе сорта железа, формы и размеров сердечников.Правда, электротехникам удавалось строить сносные по своим качествам машины и аппараты. Но это достигалось ценой бесконечных опытов, ценой долгого и утомительного подбора конструктивных размеров машин. Электротехника не была еще в те времена в полном смысле техникой. Она сохраняла в себе черты ремесла. Строгий математический расчет был вхож не во все ее области.Область же электрических явлений, в которых принимает участие железо, была своеобразным медвежьим углом электротехники, заповедником, где царствовало откровенное ремесленничество.Вектор намагничивания — магнитный момент элементарного объёма, используемый для описания магнитного состояния вещества. По отношению к направлению вектора магнитного поля различают продольную намагниченность и поперечную намагниченность. Поперечная намагниченность достигает значительных величин в анизотропных магнетиках, и близка к нулю в изотропных магнетиках. Поэтому, в последних возможно выразить вектор намагничивания через напряжённость магнитного поля и коэффициент  названный магнитной восприимчивостью: 
11)Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B ивектора намагниченности M.
В Международной системе единиц (СИ):  где  — магнитная постоянная.
В системе СГС: 
В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ0μ H в системе СИ (см.Магнитная проницаемость, также см. Магнитная восприимчивость).В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.
еорема о циркуляции магнитного поля
Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году. В 1861 годуДжеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил ее (см. ниже). Уравнение, представляющее собой содержание теоремы в этом обобщенном виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей — то есть в принципе в магнитостатике — верна теорема в первоначальном виде, сформулированном Ампером и приведенном в статье первым; для общего случая правая часть должна быть дополнена членом с производной напряженности электрического поля по времени — см. ниже). Теорема гласит[1]:
Циркуляция магнитного поля постоянных токов Эта теорема, особенно в иностранной или переводной литературе, называется также теоремой Ампера или законом Ампера о циркуляции (англ. Ampère’s circuital law). Последнее название подразумевает рассмотрение закона Ампера в качестве более фундаментального утверждения, чем закон Био — Савара — Лапласа, который в свою очередь рассматривается уже в качестве следствия (что, в целом, соответствует современному варианту построения электродинамики).Для общего случая (классической) электродинамики формула должна быть дополнена в правой части членом, содержащим производную по времени от электрического поля (см.уравнения Максвелла, а также параграф «Обобщение» ниже). В таком дополненном виде она представляет собой четвёртое уравнение Максвелла в интегральной форме.
В математической формулировке для магнитостатики теорема имеет[2]следующий вид[1][3]:  Здесь  — вектор магнитной индукции,  — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме[4]:  Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса[5].
Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы (см. диамагнетики) имагнитные моменты микрочастиц (см.например ферромагнетики).Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения (см. связанные токи), выразив его через величинунамагниченности I и введя вектор напряжённости магнитного поля  Тогда теорема о циркуляции запишется в форме[6]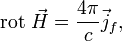  
где под  (в отличие от в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключен (что бывает удобно практически, поскольку — это обычно уже в сущности макроскопические токи, которые не связаны с намагничением вещества и которые в принципе нетрудно непосредственно измерить)[7].В динамическом случае — то есть в общем случае классической электродинамики — когда поля меняются во времени (а в средах при этом меняется и их поляризация) — и речь тогда идет об обобщенной теореме, включающей  , — всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене 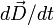 Магнитная восприимчивость и магнитная проницаемость
Ток, протекающий по проводнику, называют макротоком. Магнитное поле, создаваемое такими токами, называют полем макротоков и обозначают  . Если вещество поместить в это поле , то магнитные моменты атомов вещества будут ориентированы против поля в диамагнетике и по полю в парамагнетике. Т.е. микротоки вещества создают внутреннее поле  , противоположно направленное в диамагнетике и сонаправленное в парамагнетике. Тогда вектор магнитной индукции результирующего магнитного поля в веществе равен векторной сумме магнитных индукций внешнего поля и поля микротоков   где  .
Если рассмотреть любое сечение вещества в виде цилиндра, перпендикулярного его оси, то внутри вещества молекулярные токи соседних атомов направлены навстречу друг другу и взаимно компенсируются. Не скомпенсированными будут лишь молекулярные токи на боковой поверхности цилиндра. Ток, текущий по боковой поверхности цилиндра, подобен току в соленоиде и создает внутри него поле  N = 1; µ = 1,   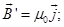   Как показывает опыт, в несильных магнитных полях намагниченность прямо пропорциональна напряженности поля  , вызывающего намагниченность  [χ] = 1где χ – безразмерная величина, называемая магнитной восприимчивостью, показывает, как вещество реагирует (намагничивается) на внешнее поле.   - связь магнитной проницаемости µ и магнитной проницаемости χ. 
Магнитная проницаемость показывает во сколько раз результирующее магнитное поле в веществе больше внешнего намагничивающего поля макротоков .
12) Классификация магнетиков. Все существующие в природе вещества по своим магнитным свойствам подразделяются на пять видов магнетиков: диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики (ферриты). В связи с тем что магнитную активность проявляют все вещества без исключения, можно утверждать, что магнитные свойства веществ определяются элементарными частицами, входящими в состав каждого атома. Такими одинаковыми для всех веществ частицами являются электроны, протоны и нейтроны. Исследования показали, что магнитные моменты протона и нейтрона почти на три порядка ниже наименьшего магнитного момента электрона, поэтому в первом приближении можно пренебречь магнитным моментом ядра, состоящего из протонов и нейтронов, и полагать, что магнитные свойства атома в целом определяются электронами. Это положение является фундаментальным в электронной теории магнетизма, которая общепринята в учении о магнетизме.Каждый атом вещества представляет собой динамическую систему, состоящую из ядра и электронного облака. Каждый электрон обладает определенным спиновым магнитным моментом  и орбитальным магнитным моментом  . С некоторой степенью упрощения можно сказать, что спиновый магнитный момент обусловлен вращением электрона вокруг собственной оси, а орбитальный − движением электрона по некоторой замкнутой орбите внутри атома. Следовательно, полный магнитный момент атома будет представлять собой геометрическую сумму орбитальных и спиновых магнитных моментов электронов, относящихся к данному атому  где z − число электронов в атоме.Рассмотрим макроскопические характеристики твердых тел, связанные с характером взаимодействия магнитных моментов с внешним полем и определяющие принадлежность данного вещества к одному из видов магнетиков [38].В любом веществе, внесенном в магнитное поле, возникает суммарный магнитный момент  , который складывается из сумм магнитных моментов  , связанных с отдельными частицами (атомами, молекулами).  Размерность магнитного момента в системе «СИ» − Вольт×секунда×метр [В×с×м] или Вебер×метр [Вб×м].
Одна из основных характеристик магнетиков – их намагниченность  Намагниченность j − векторная величина, модуль которой равен магнитному моменту единицы объема вещества. Намагниченность растет с ростом индукции магнитного поля  (или напряженности  ) в соответствии с законом
Величины æ и Как правило, по абсолютной величине магнитная восприимчивость парамагнетиков больше, чем диамагнетиков. Зависимость намагниченности этих типов магнетиков от величины напряженности магнитного поля H линейна (рис. 7.1), и при отсутствии внешнего поля она равна нулю. Интересно, что линейная зависимость j(H) для парамагнетиков имеет место только в области слабых полей и высоких температур. В сильных полях и при низких температурах j(H) выходит на насыщение js (рис. 7.2).
Кроме двух рассмотренных видов магнетиков, имеется также достаточно большая группа веществ, обладающих спонтанной намагниченностью. Они называются ферромагнетиками и имеют отличную от нуля магнитную восприимчивость ( В ряде кристаллов направления вектора магнитной индукции Найдем связь между магнитной проницаемостью и восприимчивостью вещества. Величина магнитной индукции
Для ферромагнетика результирующее поле в нем, которое и является магнитной индукцией, можно определить как (7.4) получим
|
(1) Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот, 
Подствавив (1), получим 
т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом сображении основано действие циклических ускорителей заряженных частиц. В случае, если скорость v заряженной частицы направлена под углом α к вектору В (рис. 170), то ее движение можно задать в виде суперпозиции: 1) прямолинейного равномерного движения вдоль поля со скоростью vparall=vcosα; 2) равномерного движения со скоростью vperpend=vsinα по окружности в плоскости, которая перпендикулярна полю. Радиус окружности задается формулой (1) (в этом случае надо вместо v подставить vperpend=vsinα). В результате сложения двух данных движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой (спиральной) линии 
Подставив в данное выражение (2), найдем 
Направление, в котором закручивается спираль, определяется знаком заряда частицы. Если скорость v заряженной частицы составляет угол α с направлением вектора В неоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле.
, где 
− магнитная постоянная, 
− относительная магнитная проницаемость, которая показывает, во сколько раз магнитная индукция поля в данной среде больше или меньше, чем в вакууме (в вакууме 
сонаправлен вектору напряженности внешнего магнитного поля 
). Такие вещества относятся к парамагнетикам.Если магнитная восприимчивость æ < 0, то векторы намагниченности и напряженности направлены противоположно друг другу ( 
), что характерно для диамагнетиков.
) даже в отсутствие внешнего поля. Механизм намагничивания ферромагнетиков оказывается довольно сложным, и полный цикл намагниченности ферромагнетиков описывается петлей гистерезиса (рис. 7.3).
поле в ферромагнетике складывается из напряженности внешнего магнитного поля 
cледовательно 
Выше было сказано, что магнитный момент атомов связан с движением электронов относительно своей оси и их орбитальным движением. Следовательно, существует некая жесткая связь между механическими и магнитными характеристиками атомов. Эта связь задается так называемыми гиромагнитными соотношениями. Обозначим орбитальный механический момент электрона 
, а спиновый механический момент электрона 
. Пользуясь обозначениями магнитных моментов, заданными в формуле (7.1), запишем гиромагнитные соотношения