Читайте также:
|
Частным случаем нормального распределения является логарифмически-нормальное распределение (логнормальное распределение). Функция плотности вероятности для него имеет вид:
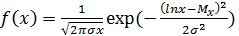(2.15.)
Вид функции плотности логнормального распределения приведен на рисунке 4.3. Данному распределению подчиняется, например, размер частиц при дроблении какого-либо материала.
Математическое ожидание и дисперсия для данного закона определяется выражениями:
, 
,
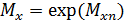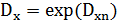Где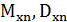 
- соответственно математическое ожидание и дисперсия нормального закона распределения 
(
- связанного с логнормальным соотношением:
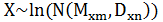
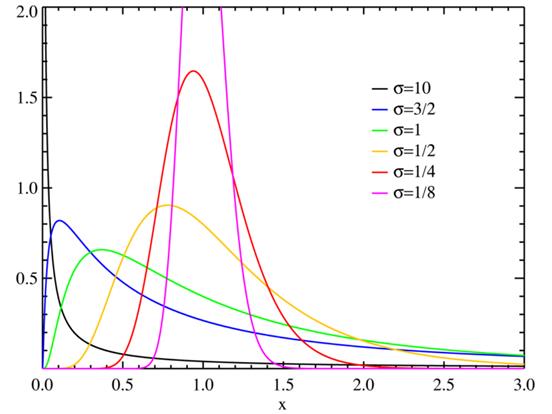
Рисунок 2.9- Плотность вероятности логнормального распределения
Еще одним из видов распределений, встречающихся при анализе экспериментальных данных в радиотехнике, являются двухпараметрические распределения: двойное экспоненциальное распределение (распределение Лапласа) и распределение Вейбулла (распределение Релея).
Функция плотности распределения для распределения Лапласа имеет вид:
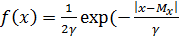) (2.16.)
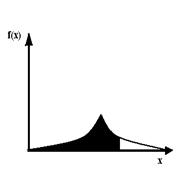
На рисунке 2.9 приведены графики функции плотности распределения и интегральной функции распределения для распределения Лапласа. С помощью двойного распределения Лапласа описываются, в частности, процессы теплообмена океана с атмосферой, а также кинетика квазихрупкого разрушения.
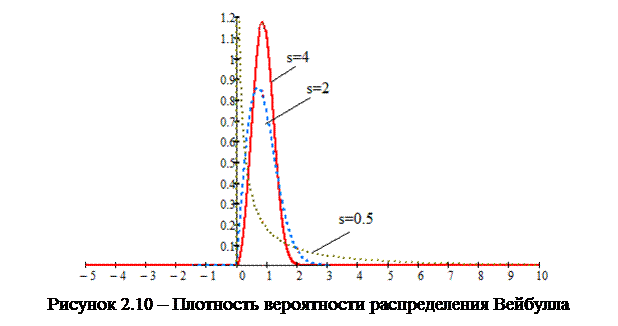
При использовании распределения Вейбулла на вид графика большое внимание оказывает параметр распределения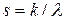 
. Чем больше значение данного параметра, тем более острую вершину имеет график. При значениях параметра, меньших единицы, график приближается к виду экспоненциальной зависимости. Данные выводы подтверждаются результатами, приведенными на рисунке 2.10.
Как отмечалось выше, наиболее простым видом распределения является равномерный закон распределения. Для него значения математического ожидания и среднеквадратического отклонения связаны с величиной интервала, в котором может изменяться случайная величина:
, 
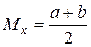. (2.17)
Правильное применение приведенных выше закономерностей, связывающих положение моментов статистического распределения и его параметров с формой графика плотности вероятности, можно быстро и эффективно выбрать гипотезы о принадлежности полученных экспериментальных данных к тому или иному закону распределения.
Для распределения Вейбулла функция плотности распределения определяется формулой:
a б
Рисунок 2.11 - Распределение Лапласа: а - функция плотности вероятности; б- интегральная функция распределения
, 
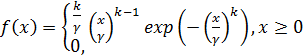(2.18.)
где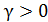 
- коэффициент масштаба, 
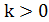-параметры распределения. Математическое ожидание и дисперсия данного распределения определяются формулами:
, 
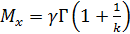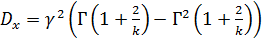. (2.19.)
В данных соотношениях Г(
- гамма-функция.
Дата добавления: 2015-02-16; просмотров: 250 | Поможем написать вашу работу | Нарушение авторских прав |
|