Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Аппроксимация, интерполяция и экстраполяция функций

Глава 9. ОБЩИЕ ВОПРОСЫ приближения функций. интерполяция функций алгебраическими многочленами

Аппроксимация, интерполяция и экстраполяция функций

По виду рассматриваемых множеств значений аргумента задачи приближения величин функций делят на два основных вида:

1) расчет значения функции в заданной точке и

2) приближение функции на отрезке вещественной оси.

Первая задача обычно решается при помощи разложения функции в ряд. Чаще всего применяется ряд Тейлора. Вторая задача более разносторонняя и требует применения особых методов решения.

Основными способами задания функциональных зависимостей являются: аналитический, графический и табличный. Табличный способ обычно используют при обработке экспериментальных данных. Основной недостаток такого способа задания функции в том, что всегда возникает необходимость определения значения зависимости при величинах переменных, которых нет в таблице. Для расчета таких значений строят вспомогательную аналитическую функцию, которая приближенно описывает зависимость, задаваемую таблицей, т.е. выполняется переход к аналитическому представлению функциональной зависимости. Приближающую функцию называют аппроксмирующей, а саму замену табличного представления аналитическим - аппроксимацией.

Рассмотренный классический случай приближенного задания функций не исчерпывает все случаи аппроксимации. Зачастую возникает необходимость приближенного задания функций F (x), уже имеющих аналитическое задание, функциями заданного вида - например, приближение тригонометрической функции алгебраическими полиномами. Также в качестве условий, которым должна удовлетворять аппроксимирующая функция, могут выступать не только ее значения в заданных точках, но и значения ее производных, условия непрерывности, гладкости и т.д. Для общности будет называть данные условия начальными или исходными.

В классическом понимании интерполированием в вычислительной математике называют способ нахождения промежуточных значений некоторой функции f (x) заданного вида (например, алгебраического многочлена) по заданному дискретному набору ее известных значений f_i = f (x_i) (i =1,2,…, n) при точном прохождении f (x) через заданные точки (x_i, f (x_i)). Построение функции f (x) называются интерполяцией. Таким образом, интерполяцию можно представить как частный случай аппроксимации, в котором заданные условия на функцию выполнены точно.

Наряду с аппроксимацией и интерполяцией также на практике часто возникают задачи экстраполяции – определения значений функциональной зависимости за пределами заданного отрезка или набора точек, т.е. продление функции.

Функция f (x), используемая для решения задачи аппроксимации или интерполяции, может быть единой кривой на всей области или состоять из отдельных кривых на заданных отрезках области, которые соединяются в крайних точках требуемым образом. Такая функция f (x) называется кусочной, а отдельные ее кривые – сплайнами.

Основной задачей аппроксимации и интерполирования функциональных зависимостейявляется построение аналитических функций требуемого вида. В общем случае вид функции заранее задан (например, алгебраический или тригонометрический полином) с точностью до некоторого набора коэффициентов {С₀,С₁,…,С _k }, входящих в ее формулу. При этом ее можно представить в виде f (x,С₀,С₁,…,С _k). Коэффициенты {С₀,С₁,…,С _k } называют параметрами синтеза, поскольку они полностью характеризующими моделируемую кривую и за счет их варьирования можно получить выполнение условий, наложенных на искомую функцию.

Таким образом, для полного определения искомой функции необходимо найти значения неизвестных коэффициентов {С₀,С₁,…,С _k }. Данный расчет выполняется на основании заданных исходных условий, под которыми в общем случае могут выступать следующие виды ограничений на искомую функцию:

- прохождение функции f (x) через заданную точку(у_i,х_i): f (х_i) = у_i;

- непрерывность функции f (x) в месте её сопряжения х_i с другой кривой: f (х_i) = g (х_i);

- равенство некоторой производной порядка j искомой функции f (x) в точке х_i некоторой заданной величине: f^j (х_i) = у_i ^j ;

- гладкость порядка j (непрерывность производной данного порядка) искомой функции f (x) в месте её сопряжения х_i с другой функцией g (х): f ^j (х_i) = g^j(х_i);

- и т.д.

Каждое из перечисленных условий задаёт ровно одно ограничение на искомую функцию f (x,С₀,С₁,…,С _k). Следовательно, на его основе можно записать одно уравнение, которое содержит неизвестные значения коэффициентов {С₀,С₁,…,С _k }, задающих функцию.

С учетом рассмотренных выше терминов, точное выполнение всех исходных условий, наложенных на искомую функциональную зависимость, можно назвать интерполяцией. Если же условия выполняются для f (x,С₀,С₁,…,С _k) приближенно, то построение называем аппроксимацией.

Интерполирование функции f (x,С₀,С₁,…,С _k), как правило, всегда возможно в том случае, когда количество параметров синтеза (k+ 1) равно либо превышает число исходных условий, наложенных на неё. В этом случае по данным условиям всегда можно составить систему уравнений относительно параметров синтеза, которая имеет хотя бы одно решение. Иначе (количество параметров синтеза меньше числа условий) в общем случае может иметь место только аппроксимация кривой по заданным условиям. Как будет показано ниже, это правило нарушается в тех случаях, когда имеет место дублирование исходных условий, налагаемых на приближенную функцию.

Наиболее распространенным является случай линейной аппроксимации (интерполирования), когда исходный набор условий либо функция приближенно (точно) заменяются функциональной зависимостью f (x,С₀,С₁,…,С _k), которая имеет вид:

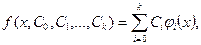(9.1)

где - постоянные коэффициенты – параметры синтеза, - семейство функций, образующих базис.

Определение. Набор функций 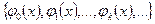образует базис, если любая достаточно гладкая функция аргумента х может быть единственным образом выражена в виде линейной комбинации базисных функций (9.1).

Единственность представления функций в форме линейной комбинации базисных функций (9.1) равносильна выполнению следующего условия: , при 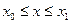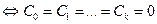, (9.2)

то есть, тождественно нулевая функция не может быть представлена разложением в семействе с ненулевыми коэффициентами. Семейство функций {j _i (t)} обычно задают заранее, исходя из более удобного и быстрого расчета формул, требований к последующим расчетам и других условий.

Наиболее часто в качестве {j _i (t)} используют степенные функции: j _i = xⁱ, i= 0, 1 ,…,n. В этом случае аппроксимирующая функция f (x,С₀,С₁,…,С _k) вида (9.1) является алгебраическим полиномом с неизвестными коэффициентами:

(9.3)

Решение задачи интерполирования при заданном базисе { j_i (t)} сводится к решению системы уравнений, получаемой при подстановке заданных геометрических условий в выражение (9.3). Метод решения, при котором коэффициенты разложения `С = { С ₀ ,С ₁ ,…,С_n } определяются непосредственным решением этой системы, называют методом неопределенных коэффициентов.

Замечание. При произвольном задании исходных условий на аппроксимирующую функцию (по количеству и виду) для точного решения задачи интерполирования в качестве переменных должны быть приняты и максимальная степень полинома k и вектор его неизвестных коэффициентов `C.

В ряде случаев при моделировании функций использование интерполирования (точного выполнения всех исходных условий) либо невозможно, либо нежелательно. В первом случае это обычно связано с тем, что максимальная степень k зафиксирована либо ограничена и ее “ не хватает” для точного выполнения всех геометрических условий. Во втором случае функция, полученная интерполированием, имеет вид, неудовлетворительный с конструктивной или эстетической точки зрения, обычно – повышенная ее осцилляция. Выход заключается в построении приближенных функций с аппроксимацией (приближенным выполнением) заданных условий либо использовании сплайнов.

При построении аппроксимирующей функции f (x,С₀,С₁,…,С _k) вида (9.1) в случае заданного базиса { j_i (t)} возможны два основных подхода:

1. Варьируются условия, накладываемые на функцию, а коэффициенты `С определяются по ним однозначно. Примером такого подхода являются функции (кривые) Безье.

2. Условия принимаются неизменными, а варьируются величины коэффициентов `С - например, при аппроксимации с помощью алгебраических полиномов).

При приближенном решении задачи в качестве критерия оптимальности выполненной аппроксимации в зависимости от решаемой задачи могут быть приняты:

- численные характеристики близости функции f (x,С₀,С₁,…,С _k) к заданным геометрическим условиям;

- эстетический вид получаемой функции f (x,С₀,С₁,…,С _k), который субъективно оценивается пользователем.

В качестве численной меры близости моделируемой функции f (x,С₀,С₁,…,С _k) к заданной на интервале [ a,b ] функции F (x)наиболее часто применяют две характеристики:

1) максимальное абсолютное отклонение

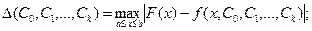(9.4 a)

2) среднеквадратичная ошибка

_. (9.4 б)

Более точно отражают геометрическую близость функций разности, взятые не по параметру x, а по нормали к графику исходной функции F (x), однако вычисление таких ошибок более сложно. В том случае, если моделируется кривая, которая должна пройти вблизи заданных точек (у ₁ ,х ₁),(у ₂ ,х ₂),…,(у_n,х_n), то критерии (9.4а) и (9.4б) заменяют, соответственно, на следующие величины:

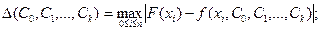(9.5 а)

(9.5 б)

В обоих рассмотренных случаях требуется за счёт варьирования величин коэффициентов `С достичь минимально возможной величины соответствующей численной характеристики отклонения. В математической форме критерии оптимального синтеза аппроксимируемых кривых по обеим характеристикам близости принимают одинаковый вид:

d (С₀, …, С_k) ® min (С₀, …, С_k); D (С₀, …, С_k) ® min (С₀, …, С_k).

Очевидно, интерполирование может рассматриваться как частный случай аппроксимации, при котором величина отклонения равна нулю.

Вопросы для проверки знаний.

1. Назовите основные способы задания функциональных зависимостей.

2. Какую традиционную задачу представления функциональных зависимостей называют аппроксимацией?

3. Какую задачу приближения функциональных зависимостей в общем случае называют интерполяцией?

4. Какую задачу приближения функциональных зависимостей называют экстраполяцией?

5. Какую функцию, используемую для решения задачи аппроксимации или интерполяции функциональных зависимостей, называют кусочной?

Что называют сплайнами?

6. В какой форме обычно представляют приближающую функцию требуемого вида?

7. Какие исходные условия могут быть заданы для приближающей функции в общем случае? Что называют параметрами синтеза?

8. Что называют линейной аппроксимацией (интерполированием)?

9. Какой набор функций называют базисом?

10. В чем заключается метод неопределенных коэффициентов при расчете параметров синтеза?

11. Какие два подхода применяют при построении аппроксимирующей функции в случае заданного базиса?

12. Какие две численные характеристики наиболее часто применяют для оценки близости моделируемой функции к заданной функции на интервале или на множестве точек?