|
Читайте также: |
Рассмотрим случай, когда требуется обеспечить прохождение алгебраической кривой через заданные точки `P 0 = (x 0 ,y 0), `P 1 = (x 1 ,y 1) ,...,`Pn= (xn,,yn), (условия типа 1 в общей постановке задачи узлового интерполирования). На производные в данных точках никаких условий не накладывается. Узлы этого типа называют однократными, поскольку в них задано одно геометрическое условие. Такая задача на практике возникает в тех случаях, когда 1) требуется провести степенную кривую через набор точек либо 2) заменить функцию f (х)произвольного вида степенной Р (х)при заданных положениях абсцисс её узлов x 0, x 1 ,..., xn.
В математической форме задачу интерполирования по однократным узлам можно сформулировать следующим образом. В узлах xi, (i = 0,1 ,...,n; xi ¹ xj при i¹ j)заданы значения у (xi) =уi. Требуется построить полином Р (x) минимально возможной степени, для которого Р (xi) = уi, (i = 0,1 ,...,n).
Решение задачи существует и единственно, хотя сам многочлен может быть представлен в разных видах. Наряду с каноническим представлением (9.6) в задаче интерполирования по однократным узлам он может быть представлен в виде полиномов Лагранжа и Ньютона.
Так как общее число геометрических условий в задаче равно n+1, то искомый интерполяционный полином имеет степень не выше n (при этом число его неизвестных коэффициентов C 0, C 1, …, Cn равно n+ 1). Примеры, в которых степень полинома меньше расчётной, рассмотрены в п.9.2.
В явных решениях задачи используется полином w(х), принимающий однократные нулевые значения только в узлах интерполирования x0, x1,..., xn и имеющий единичный коэффициент при старшей степени х. Его можно представить в виде: w (х) = (x-x 0)× (x- x 1) ×... × (x- xn).
 |
При подстановке в производную узловой точки xi все слагаемые кроме i -го обнуляются и получается произведение, в котором отсутствует i -тый сомножитель:
w¢ (xi) = (xi -x 0) × (xi - x 1) ×... × (xi - xi- 1)× (xi - xi+ 1) × …× (xi - xn).
Рассмотрим явное решение Лагранжа задачи интерполирования по однократным узлам. В основе его лежит использование функций Лагранжа Фi (x)(i = 0,1 ,...,n), которые выделяют соответствующий узел:
Построение каждой функции Фi (x)можно представить следующим образом. Полином, принимающий нулевые значения в узлах x 0, x 1 ,..., xi- 1, xi+ 1 ,… xn и имеющий единичный коэффициент при старшей степени имеет вид:
w (х)/(x-xi) = (x-x 0) × (x - x 1) ×... × (x - xi- 1)× (x - xi+ 1)× …× (x - xn).
В узле х=xi значение его равно некоторой ненулевой константе: w¢ (xi) = (xi -x 0)× (xi - x 1)× ...× (xi - xi- 1)× (xi - xi+ 1) × …× (xi - xn), которая в общем случае может принять любое ненулевое значение (как по величине так и по знаку). Для того, чтобы искомая функция в узле х=xi стала равной единице, необходимо w (х)/(x-xi)разделить на w¢ (xi):
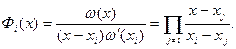(9.10)
Полученные функции Лагранжа Фi (x) (9.10)обладают всеми требуемыми свойствами. Интерполяционный многочлен Лагранжа имеет вид:
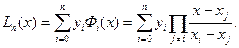(9.11)
Выражение (9.11) в векторной форме можно представить как скалярное произведение:
L n (x) = (`Ф (х) ,`Y), (9.12)
где `Y= (y 0, y 1 ,..., yn); `Ф (х) = (Ф 0(х), Ф 1 (х) ,..., Фn (х)).
Рассмотрим простейший случай интерполирования на отрезке [ x 0, x 1].В его граничных точках заданы по одному геометрическому условию: у (x 0) = у 0, у (x 1) = у 1. Наименьшая степень полинома S (x)равна единице. Явное решение для S (x)даёт следующий многочлен Лагранжа:
S (x) = у 0(x 1 –x)/(x 1 -x 0) + у 1(x-x 0)/(x 1 -x 0 ).(9.13)
В векторной форме:
S (x) = (`Ф (x) ,`Y);(9.14)
где `Ф (x) = ((x 1 –x)/(x 1 -x 0), (x-x0)/(x 1 -x 0 )); `Y= (у 0, у 1).
Переходя к безразмерной нормированной переменной t= (x-x 0)/(x 1 -x 0), у которой t (x 0)=0; t (x 1)=1, получим более простые выражения для функций Лагранжа: Ф 1(t) = 1 -t; Ф 2(t) = t. Введём также вектор `T 1 степеней t порядка 1 и матрицу МЛ, задающую переход от `T 1 к вектору значений функций Лагранжа (Ф 1 (t); Ф 2 (t)):
 |
(9.15)
Данное представление помогает унифицировать интерполяцию кривой отрезком прямой на произвольном интервале и используется при сплайновом интерполировании.
Для уменьшения трудоемкости расчета значений полинома Лагранжа в слагаемых формулы (9.11) выделим постоянные сомножители, которые обозначим l i:
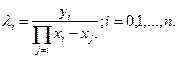(9.16а)
При этом формула (9.11) принимает вид:
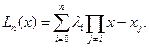(9.16б)
Непосредственный расчет одного слагаемого в формуле (9.16б) требует выполнения n вычитаний и n умножений. Вычисление всех (n +1) слагаемых и их суммирование требует в сумме примерно (n +1)2 сложений и вычитаний, а также примерно (n +1)2 умножений. Сложность такого вычисления квадратичная по числу узлов - О((n +1)2).
Однако если использовать пересчет произведений в подряд стоящих слагаемых:
то для полного расчета формулы (9.16б) потребуется примерно: 3(n +1) умножений, 4(n +1) сложений и вычитаний, (n +1) делений. Сложность такого вычисления линейная по числу узлов - О((n +1)1).
Для еще большего снижения трудоемкости расчета значений полинома Лагранжа можно привести его к каноническому виду и вычислять по схеме Горнера, затрачивая примерно (n +1) умножений и (n +1) сложений. Полученный в результате полином канонического вида совпадает с решением, получаемым по методу неопределенных коэффициентов. Но при этом алгоритм его определения упрощается.
Пример 1. На множестве однократных узлов x 0= -1; x 1 = 2; x 2 =4заданы значения функции у (x): у (x 0) = у 0 = - 2; у (x 1) = у 1 = 1; у (x 2) = у 2 = 5. Построить функции, многочлен Лагранжа и привести его к каноническому виду.
Решение. Вспомогательный полином w (х) имеет вид:
w (х) = (x-x 0)(x- x 1)(x- x 2 ) = (x+ 1)(x- 2)(x- 4).
Функции Лагранжа строим по формуле (9.10):
Многочлен Лагранжа строим по формуле (9.11):
В векторной форме: L 2(x)=(`Ф (х) ,`Y), где `Ф (х) = (Ф 0(х), Ф 1(х), Ф 2(х)) =
`Y = (y 0, y 1, y 2) = (-2, 1, 5).
В полученном скалярном выражении для L 2(x) раскрываем все произведения и после приведения членов получим канонический вид решения:
L 2(x) = - 2(x 2-6 x +8)/15 - (x 2-3 x -4)/6+(x 2 - x -2)/2 =
= 0,2 x 2×[-2/15-1/6+1/2]+ x ×[12/15+3/6-1/2]+[-16/15+4/6-2/2] = 0,2 x 2 + 0,8 x -1,4.
При интерполировании большого числа (n +1) узловых точек единым полиномом Ln (x) его значения на промежутках между узлами сильно отклоняются от значений в самих узлах. Данное явление называют осцилляцией интерполирующего полинома. Полиномы такого вида, как правило, недопустимы в практических приложениях, поскольку требуется построить кривую, плавно соединяющую узловые точки. Поэтому в таких случаях применяют другие методы приближения.
Вопросы для проверки знаний.
1. Какие узлы в теории интерполирования функций одной переменной называют однократными?
2. Какую минимальную степень имеет полином, точно решающий задачу интерполирования по однократным узлам `P 0 = (x 0 ,y 0), `P 1 = (x 1 ,y 1) ,...,`Pn = (xn,,yn) и в каком виде он может быть представлен?
3. Какие условия накладываются на функции Лагранжа и какую структуру имеют данные функции?
4. Как на основе функций Лагранжа строится полином Лагранжа?
5. Поясните вывод функций Лагранжа и построение полинома Лагранжа для простейшего случая интерполирования по двум однократным узлам.
6. Что называют матрицей Лагранжа? Какой вид она имеет?
7. Какова трудоемкость и сложность вычисления значений полинома по формуле Лагранжа при полном расчете и с пересчетом произведений в слагаемых полинома? Что можно сделать для ее дальнейшего снижения?
8. Какое явление называют осцилляцией интерполирующего полинома?
Дата добавления: 2015-02-16; просмотров: 198 | Поможем написать вашу работу | Нарушение авторских прав |