Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Затухающие колебания.

Во всякой реальной колебательной системе имеются силы сопротивления, действие которых приводит к уменьшению энергии системы. Если убыль энергии не восполняется за счет работы внешних сил, колебания будут затухать. В простейшем, и вместе с тем наиболее часто встречающемся, случае сила сопротивления F * пропорциональна величине скорости:

. (3.18)

Здесь r — постоянная, называемая коэффициентом сопротивления. Знак минус обусловлен тем, что сила F * и скорость v имеют противоположные направления; следовательно, их проекции на ось x имеют разные знаки.

Уравнение второго закона Ньютона при наличии сил сопротивления имеет вид

. (3.19)

Применив обозначения

(3.20)

ω₀ ‑ представляет собой ту частоту, с которой совершались бы свободные колебания системы в отсутствие сопротивления среды (при r = 0). Эту частоту называют собственной частотой системы.

перепишем уравнение (3.19) следующим образом:

. (3.21)

Подстановка в (3.21) функции x = e ^{λ t} приводит к характеристическому уравнению

(3.22)

Корни этого уравнения равны

, . (3.23)

При не слишком большом затухании (при β<ω₀) подкоренное выражение будет отрицательным. Представим его в виде (iω)², где ω — вещественная величина, равная

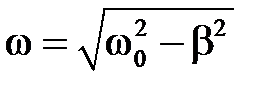. (3.24)

Тогда корни характеристического уравнения запишутся следующим образом:

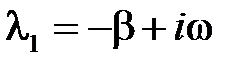, . (3.25)

Общим решением уравнения (58.1) будет функция

.

Таким образом, при не слишком сильном затухании общее решение уравнения (3.21) имеет вид

. (3.26)

Здесь a₀ и α — произвольные постоянные, ω — величина, определяемая формулой (3.24). На рис. дан график функции (3.26). Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки x.

В соответствии с видом функции (3.26) движение системы можно рассматривать как гармоническое колебание частоты ω с амплитудой, изменяющейся по закону a (t) = a ₀ e ^{‑β∙ t} . Верхняя из пунктирных кривых на рис. дает график функции a (t), причем величина a ₀ представляет собой амплитуду в начальный момент времени. Начальное смещение x ₀ зависит, кроме a ₀, также от начальной фазы α: x ₀ = a ₀∙cosα.

Скорость затухания колебаний определяется величиной β = r /2 m, которую называют коэффициентом затухания. Найдем время τ, за которое амплитуда уменьшается в e раз. По определению e ^‑β∙τ = e ^‑1, откуда β∙τ = 1. Следовательно, коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшается в e раз.

Согласно формуле (3.24) период затухающих колебаний равен

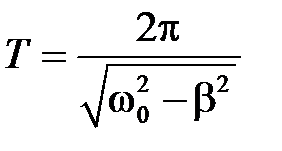. (3.27)

При незначительном сопротивлении среды () период колебаний практически равен T ₀ = 2π/ω₀. С ростом коэффициента затухания период колебаний увеличивается.

Последующие наибольшие отклонения в какую-либо сторону (например, a ', a '', a ''' и т.д. на рис. образуют геометрическую прогрессию. Действительно, если a ' = a ₀ e ^{‑β∙ t} , то a '' = a ₀ e ^{‑β(t + T)} = a ' e ^{‑β T} , a ''' = a ₀ e ^{‑β(t +2 T)} = a '' e ^{‑β T} и т. д. Вообще, отношение значений амплитуд, соответствующих моментам времени, отличающимся на период, равно

.

Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания:

(3.28)

(не путать с λ в формулах (3.23) и (3.25)!).

Для характеристики колебательной системы обычно используется логарифмический декремент затухания λ. Выразив в соответствии с (3.28) β через λ, и T, можно закон убывания амплитуды со временем записать в виде

.

За время τ, за которое амплитуда уменьшается в е раз, система успевает совершить N_e = τ/ T колебаний. Из условия получается, что . Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в e раз.

Для характеристики колебательной системы часто употребляется также величина

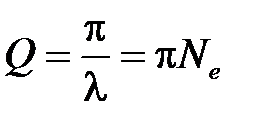, (3.29)

называемая добротностью колебательной системы. Как видно из ее определения, добротность пропорциональна числу колебаний N_e, совершаемых системой за то время τ, за которое амплитуда колебаний уменьшается в e раз.

Подстановка функции (58.7) и ее производной в выражение для полной энергии колеблющейся системы E = kx ²/2 + mv ²/2 приводит после преобразований к формуле

, (3.30)

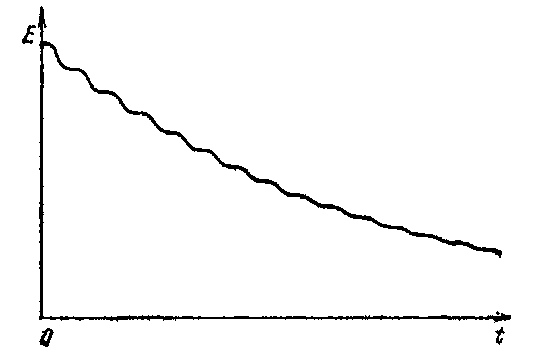где y = arctg (β/ω). График этой функции изображен на рис. Убывание энергии обусловлено работой силы сопротивления среды . Мощность, развиваемая этой силой, равна . Таким образом,

.

Отсюда вытекает, что в тех точках кривой E (t), где , касательная к кривой параллельна оси t. В остальных точках dE / dt < 0.

При малом затухании (β<<ω₀) слагаемым, содержащим синус, в формуле (3.30) можно пренебречь и считать, что энергия изменяется по закону

E = E ₀ e ^{‑2β t} , (3.31)

где E ₀ = k (a ₀)²/2 — значение энергии в начальный момент. К тому же результату можно прийти, если заменить определяемое формулой (3.30) мгновенное значение E (t) его средним значением за времяот t — T /2 до t + T /2 (T — период колебаний), вычисленным в предположении, что множитель ехр (—2β t) в течение промежутка T остается постоянным.

Из формулы (3.27) следует, что с ростом коэффициента затухания период колебаний увеличивается. При β=ω₀ период колебаний обращается в бесконечность, т. е. движение перестает быть периодическим.

При β>ω₀ корни характеристического уравнения становятся вещественными (см. (3.25)) и решение дифференциального уравнения (3.21) оказывается равным сумме двух экспонент:

.

Здесь C ₁ и C ₂ — вещественные постоянные, значения которых зависят от начальных условий (от x ₀ и v ₀).Следовательно, движение носит апериодический (непериодический) характер— выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.

На рис.показано оба возможных способа возвращения системы к положению равновесия при апериодическом движении. Каким из этих способов приходит система в положение равновесия, зависит от начальных условий. Движение, изображаемое кривой 2, получается в том случае, когда система начинает двигаться из положения, характеризуемого смещением x ₀, к положению равновесия с начальной скоростью v ₀ определяемой условием

. (3.32)

Это условие будет выполнено в том случае, если выведенной из положения равновесия системе сообщить достаточно сильный толчок к положению равновесия. Если, отведя систему из положения равновесия, отпустить ее без толчка (т. е. с v ₀=0) или сообщить ей толчок недостаточной силы (такой, что v ₀ окажется меньше определяемой условием (3.32)), движение будет происходить в соответствии с кривой 1 на рис.