Читайте также:
|
Колебательное движения (определение). Гармонические колебания и их характеристики (амплитуда, фаза, частота, период).Дифференциальное уравнение гармонических колебаний и его решение.
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т. Д
Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воз действий на колебательную систему (систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания — колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса). Рассмотрение гармонических колебаний важно по двум причинам:
1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому;
2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа
(140.1)
где А — максимальное значение колеблющейся величины, называемое амплитудой колебания, w 0 — круговая (циклическая) частота, j — начальная фаза колебания в момент времени t = 0, (w0t + j)— фаза колебания в момент времени t.
Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до - 1, то s может принимать значения от + Адо - А .
Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебания, за который фаза колебания получает приращение 2p, т. е.
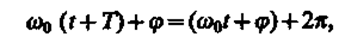
откуда
(140.2)
Величина, обратная периоду колебаний,
(140.3)
т. е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (140.2) и (140.3), получим
Единица частоты — герц (Гц): 1 Гц — частота периодического процесса, при которой за 1 с совершается один цикл процесса.
Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:
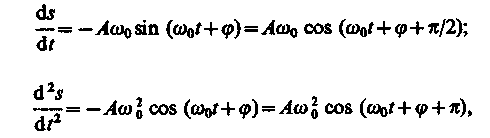(140.4) (140.5)
т. е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (140.4) и (140.5) соответственно равны Аw0 и Аw20.Фаза величины (140.4) отличается от фазы величины (140.1) на p/2, а фаза величины (140.5) отличается от фазы величины (140.1) на p. Следовательно, в моменты времени, когда s = 0, ds/dtприобретает наибольшие значения; когда же s достигает максимального отрицательного значения, то d2s/dt2 приобретает наибольшее положительное значение (рис. 198). 
Рис. 198
Из выражения (140.5) следует дифференциальное уравнение гармонических колебаний
(140.6)
(где s = A cos (w0t + j)). Решением этого уравнения является выражение (140.1).
(140.1)
Дата добавления: 2015-01-30; просмотров: 83 | Поможем написать вашу работу | Нарушение авторских прав |