Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Эффект Доплера для звуковых волн

Пусть источник, находящийся в газе или жидкости, испускает короткие импульсы с частотой ν. Если источник и приемник покоятся относительно среды, в которой распространяется волна, то частота воспринимаемых приемником импульсов будет равна частоте ν источника. Если же источник, или приемник, или оба движутся относительно среды, то частота ν', воспринимаемая приемником, вообще говоря, оказывается отличной от частоты источника: ν' ¹ ν. Это явление называют эффектом Доплера.

Сначала рассмотрим случай, когда источник S и приемник P движутся вдоль проходящей через них прямой с постоянными скоростями u и u ' соответственно (относительно среды).

Если бы двигался только источник навстречу приемнику, испуская импульсы с периодом T = 1/ν, то за это время очередной импульс пройдет относительно среды расстояние λ = v ∙ T, где v — скорость волн в среде, и пока будет испущен следующий импульс, источ ник «нагонит» предыдущий импульс на расстояние uT. Таким образом, расстояние между импульсами в среде станет равным λ' = vT – uT (рис.), и воспринимаемая неподвижным приемником частота (число импульсов за единицу времени)

.

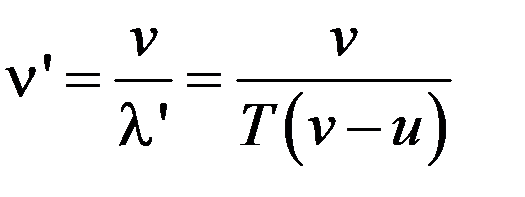Если же движется и приемник (пусть тоже навстречу источнику, то импульсы относительно приемника будут иметь скорость v + u ', и число воспринимаемых за единицу времени импульсов

.

Нетрудно сообразить, что при движении как источника, так и приемника в противоположных направлениях, знаки перед u ' и u надо поменять на обратные. Еще раз подчеркнем, что скорости u ' и u — это скорости приемника и источника относительно среды.

Как видно из приведенных рассуждений, эффект Доплера является следствием «уплотнения» (или разряжения) импульсов, обусловленным движением источника и приемника.

Формулу целесообразнее записать в иной форме, более общей и более простой для запоминания и использования:

u ' _x и u_x – проекции скоростей приемника и источника на ось X, проходящую через них и положительное направление которой совпадает с направлением распространения импульсов, т. е. от источника S к приемнику P.

Прежде чем продолжить обсуждение возможностей выражения (1.60), приведем два простых примера.

Пример 1. Источник S и приемник P удаляются друг от друга по одной прямой в противоположные стороны относительно среды со скоростями u и u '. Частота источника ν, скорость сигналов в среде v. Найдем частоту v ', воспринимаемую приемником.

В данном случае проекция скорости приемника на ось X есть u '_х = u ', а проекция скорости источника u_x = - u. Подставив эти величины в формулу (1.60), получим

ν' = ν (v - u ')/(v + u).

Пример 2. Источник S, испускающий сигналы с частотой ν, движется с постоянной скоростью u_s относительно приемника P, установленного на башне (рис.). При этом воздушная масса перемещается относительно земной поверхности вправо с постоянной скоростью u ₀ (ветер). Скорость звука в воздухе v. Найдем частоту v ', воспринимаемую приемником.

Имея в виду, что в формулу входят скорости относительно среды, запишем: проекция скорости приемника u '_х = – u ₀, а проекция скорости источника u _х = u_s – u ₀. Обе проекции взяты, как должно быть, на ось X, направленную вправо. Остается подставить эти проекции в формулу (1.60), и мы получим: