Читайте также:
|
Механическое движение. Виды мех. движения.
Мех. движение – это изменение с течением времени взаимного расположения тел или их частей. Виды движения: 1). Поступательное – движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. 2). Вращательное – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. 3). Колебательное – движение характеризующееся некоторой степенью повторяемости во времени.
Система отсчета. Скорость и ускорение как производные радиус-вектора. Нормальная и тангенциальная составляющая вектора ускорения.
Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел. 1. Скорость и ускорение материальной точки как производные радиуса-вектора по времени. Положение точки определяется пространственными параметрами: радиус-вектором, декартовыми координатами, дуговой координатой и др. Скорость точки является пространственно - временным параметром. Скоростью точки называется кинематический параметр, характеризующий быстроту изменения положения точки в системе отсчета с течением времени. v=S/t
v=v0+a*t
a=(v-v0)/t Тангенциальное или касательное ускорение 
(обозначается иногда 
и т. д., в зависимости от того, какой буквой в конкретном тексте принято обозначать ускорение) направлено по касательной к траектории. Является составляющей вектора ускорения 
коллинеарной вектору мгновенной скорости. Характеризует изменение скорости по модулю.
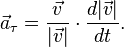
Центростремительное или нормальное ускорение 
(также обозначается иногда 
и т. д.) возникает (не равно нулю) всегда при движении точки не только по окружности, но и по любой траектории с ненулевой кривизной. Является составляющей вектора ускорения перпендикулярной вектору мгновенной скорости. Характеризует изменение скорости по направлению. Вектор нормального ускорения всегда направлен к мгновенной оси вращения,
а модуль равен
где ω — угловая скорость относительно центра вращения, а r — радиус окружности.
Кроме этих двух компонент, используется также понятие угловое ускорение, показывающее, на сколько изменилась угловая скорость за единицу времени, и, аналогично линейному ускорению, вычисляемое следующим образом:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и угловой скорости сонаправлены (или хотя бы их скалярное произведение положительно), значение скорости растёт, и наоборот.
В частном случае равномерного движения по окружности векторы углового ускорения и тангенциального ускорения равны нулю, а центростремительное ускорение постоянно по модулю.
Движение материальной точки по окружности кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является кругом, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью) Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть T, то угловая скорость вращения ω будет равна: 
Скорость движения объекта равна 
Угол поворота θ за время t равен: 
3.
Дата добавления: 2015-01-30; просмотров: 108 | Поможем написать вашу работу | Нарушение авторских прав |