Читайте также:
|
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы если
| Работа |
 *cos𝛼
|
Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени[1].
Различают среднюю мощность за промежуток времени 
и мгновенную мощность в данный момент времени:
|
7. Энергия: кинетическая и потенциальная. Закон сохранения энергии. Соотношение Эйнштейна
Эне́ргия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему[1], энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта.одних форм в другие.
Потенциальная энергия 
— скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил
Потенциальная энергия тела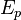 
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
где 
— масса тела, 
— ускорение свободного падения, 
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.
Закон сохранения энергии. Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной. Энергия может передаваться от одних тел к другим, а также превращаться из одного вида в другой.
- Полная механическая энергия.
Закон сохранения энергии: в замкнутой системе тел полная энергия не изменяется при любых взаимодействиях внутри этой системы тел. Закон накладывает ограничения на протекание процессов в природе. Природа не допускает появление энергии ниоткуда и исчезание в никуда. Возможно оказывается только так: сколько одно тело теряет энергии, столько другое приобретает; сколько убывает одного вида энергии, столько к другому виду прибавляется.
В механике для определения видов энергии необходимо обратить внимание на три величины: высоту подъема тела над Землей h, деформацию х, скорость тела v.
Соотношение Эйнштейна.
где 
— коэффициент диффузии, 
— подвижность частиц, 
— постоянная Больцмана, а 
— абсолютная температура.
Величина подвижности определяется из соотношения
где 
— стационарная скорость перемещения частицы в вязкой среде под действием силы 
.
Это уравнение является частным следствием флуктуационно-диссипационной теоремы.
Закон сохранения импульса. Центр масс.(Лекция) Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом[2]:
где 
— радиус-вектор центра масс, 
— радиус-вектор i -й точки системы, 
— масса i -й точки.
Для случая непрерывного распределения масс:
где 
— суммарная масса системы, — объём, 
— плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц.
Можно показать, что если система состоит не из материальных точек, а из протяжённых тел с массами 
, то радиус-вектор центра масс такой системы 
связан с радиус-векторами центров масс тел 
соотношением[3]:
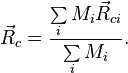
Иначе говоря, в случае протяжённых тел справедлива формула, по своей структуре совпадающая с той, что используется для материальных точек.
8.
9,Момент инерции. Момент силы. Уравнение динамики вращательного движения твердого тела. Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м². Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
· mi — масса i -й точки,
· ri — расстояние от i -й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
dm = ρ dV — масса малого элемента объёма тела dV,
ρ — плотность,
r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. 
где 
— сила, действующая на частицу, а 
— радиус-вектор частицы.
М=j*ейпсилон –уравнение динамики вращательного движения
9.
10,Момент импульса. Закон сохранения момента импульса.: Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r - радиус-вектор, проведенный из точки О в точку A, p =m v - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р. Модуль вектора момента импульса
Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.
Можно показать, что имеет место векторное равенство
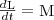(3)
В замкнутой системе момент внешних сил 
и 
откуда
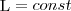(4)
Выражение (4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
10.
11.Линии и трубки тока. Неразрывности струи.Течение жидкости характеризуется линиями тока. Это линии, касательные к которым совпадают с направлением вектора скорости частиц жидкости в данной точке (см.рис.1). Часть пространства, ограниченная линиями тока, называется трубкой тока (на рисунке заштрихована). Если при течении жидкости линии тока непрерывны, то такое течение называется ламинарным (рис.1). При определенных условиях в движущейся жидкости могут возникать завихрения, скорость ее частиц хаотически изменяется, линии тока претерпевают разрывы, изменяющиеся со временем. Такое движение жидкости называется турбулентным. Непрерывности струи: Поскольку dQ = S·u·dt, то выполняется соотношение:
S1·u1 = S2·u2 или
S·u = const. (14.4)Его физический смысл заключается в том, что жидкость нигде не накапливается, т. е. за одинаковый временной интервал в трубку тока втекает и вытекает равное количество жидкости.
Уравнение Бернулли. Статистическое и динамическое давление. Закон (уравнение) Бернулли является (в простейших случаях[1][2][3][4]) следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
Здесь
— плотность жидкости,
— скорость потока,
— высота, на которой находится рассматриваемый элемент жидкости,
— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
— ускорение свободного падения.
Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает
12.
Дата добавления: 2015-01-30; просмотров: 160 | Поможем написать вашу работу | Нарушение авторских прав |