
Читайте также:
|
Наиболее распространенный коэффициент корреляции. Предназначен для расчета силы и направления линейной зависимости между переменными исследования.
Смысл коэффициента линейной корреляции.
Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной шкале либо в шкале отношений.
Если представить две переменные на координатном поле, то каждая пара значений будет отображать координаты точки в этом поле. Чем ближе точки к усредненной прямой, тем выше коэффициент корреляции (см. следующий рисунок),.

Коэффициент корреляции будет положительным числом, когда при повышении X происходит повышение Y (прямопропорциональная связь), отрицательным при обратнопропорциональной связи. На иллюстрации изображены различные по силе положительные коэффициенты корреляции.
На следующей иллюстрации видны специально сгенерированные формы зависимостей и коэффициенты корреляции для них.

Как видим, линейный коэффициент корреляции срабатывает лишь при линейном характере взаимосвязи переменных.
Общая формула:
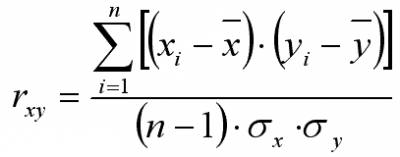
Где xi и yi - сравниваемые количественные признаки, n – число сравниваемых наблюдений, σx и σy – стандартные отклонения в сопоставляемых рядах.
Для расчетов вручную используется преобразованная формула:

Несмотря на кажущуюся громоздкость формулы, она значительно облегчает ручной расчет.
Иллюстрация расчетов:

Полученный коэффициент корреляции проверяется на значимость с помощью таблицы критических значений. Для этого вычисляем количество степеней свободы df=N-2 и на пересечении с необходимым уровнем значимости находим критическое значение коэффициента. В нашем случае df=8, уровень значимости выбираем 0,1. Получаем критический коэффициент r=0.54. Так как 0,69 > 0,54 делаем вывод о значимой корреляции (r=0,69;p≤0,1).
Дата добавления: 2015-02-16; просмотров: 116 | Поможем написать вашу работу | Нарушение авторских прав |