Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Матрицы. Размерность матрицы. Специальные матрицы (нулевая,

Единичная, квадратная).

Множество действительных чисел R. Матрицей называется прямоугольная таблица чисел. Размерностью матрицы называется пара чисел, обозначаемая mхn, где m – количество строк, n – количество столбцов. Общий вид матрицы следующий: A= 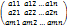=(a_ij)_mxn.

Множество всех матриц размерности mxn обозначается Мmxn (R). Две матрицы А и В одинаковой размерности называются равными, если соответствующие элементы этих матриц равны. При этом пишут А=В.

Нулевая матрица – это матрица размерности mxn, все элементы которой равны нулю. Нулевая матрица, и только она, имеет ранг=0. Это означает, что только нулевая матрица обладает свойством давать нулевой столбец при умножении справа на любой вектор-столбец, и аналогично для умножения вектор-строки слева. Единичная матрица – квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю. Матрица, в которой количество строк совпадает с количеством столбцов называется квадратной.

Сложение матриц, свойства.

Сумма матриц А и В ϵ Мmxn называется матрица А+В, которая получается путем сложения соответствующих элементов матриц А и В. Свойства сложения матриц: Пусть А, В, С ϵ Мmxn. 1) А+В=В+А 2) (А+В)+С=А+(В+С) 3) А+Ѳ=А, где Ѳ-матрица, элементами которой являются нули (нулевая матрица).

Умножение матрицы на число, свойства.

Произведение матрицы А ϵ Мmxn на число α ϵ R, называется матрица, обозначаемая αА, которая получается путем умножения всех элементов матрицы А на число α. Свойства умножения матрицы на число: Пусть А, В ϵ Mmxn и α, β ϵ R. 1) α(βА)=(αβ)А 2) α(А+В)=αА+αВ 3) (α+β)А=αА+βА 4) 1А=А 5) 0А=Ѳ 6) αѲ=Ѳ.