|
Читайте также: |
Вивчення інтегралів від виразу (4) при довільних коефіцієнтах a, b, c,…, звичайно, важко. Тому є природнім бажання звести усі ці інтеграли до небагатьох таких, до складу яких би входило при можливості менше довільних коефіцієнтів (параметрів).
це досягається за допомогою елементарних перетворень:
1. Зазначимо, на сам перед, що достатньо обмежитися випадком многочлена 4- го ступеня під коренем, адже до нього легко приводиться і випадок, коли під коренем многочлен 3- го ступеня. Дійсно, многочлен 3- го ступеня a 
+b 
+cx+d з дійсними коефіцієнтами необхідно має дійсний корінь, скажімо, λ- і,звідси випливає, припускає дійсний розклад
a +b +cx+d=a(x- λ)( +px+q).
Підстановка x- λ= 
(bkb x- λ=- ) і приводить нас до інтегралу
∫R(x, 
)dx= ∫R( + λ, t 
)2tdt.
2. Многочлен четвертого ступеня з дійсними коефіцієнтами можуть бути представленими у вигляді добутку двох квадратних трьохчленів з дійсними коефіцієнтами:
a 
+b +c +dx+e=a( +px+q)(
+p'x+q'). (5)
Спробуємо тепер належною підстановкою знищити в обох тричленах одразу члени першого ступеня.
Якщо p=p', то наша ціль досягається простою підстановкою x=t- 
. нехай тепер p≠p'; у цьому випадку ми скористуємося дробно- лінійною підстановкою x= 
.
Можливість встановити дійсні і при тому різні значення для коефіцієнтів μ та ν, як ми бачили, обумовлена нерівністю (
-(p-p')(p'q-pq')>0. (6)
Ми вже довели, що ця нерівність у припущені, що один із тих тричленів, що розглядають має уявні корені, і це відігравало важливу роль у наших міркуваннях. Нехай тепер тричлени (5) обидва мають дійсні корені, скажімо, перший- корені α і β, а другий- корені γ і δ. Підставивши
p=-(α+β), q=αβ, p'=-(γ+δ), q'=γδ,
можна переписати (6) у вигляді
(α-γ)(α-δ)(β-γ)(β-δ) >0, (6')
а для здійснення цієї нерівності досить лише потурбуватися, щоб корені тричленів не перемежалися (аби α>β>γ>δ).
Таким чином, правильно обравши μ і ν, за допомогою вказаної підстановки ми отримаємо
∫R(x, 
)dx=∫R (, 
) 
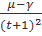dt,
що також (якщо виключити випадки виродження, коли будь- який із коефіцієнтів M, N, M',N' виявляється нулем) можна переписати у вигляді
∫ 
(t, 
)dt,
При A, m та m' відмінних від нуля.
3. За допомогою попередніх міркувань, можна звести цей інтеграл з точністю до інтеграла від раціональної функції, до такого:
∫ 
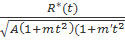dt.
Розкладемо тепер раціональну функцію 
на два доданки
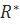(t)= 
+ 
.
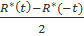Перший не змінює свого значення при заміні t на –t, звідси випливає, що він зводиться до раціональної функції від : 
(); другий при вказаній заміні змінює знак, а тому має вид 
(
.
Інтеграл, який ми розглядаємо можна представити в формі суми інтегралів
∫ 
+∫ 
.
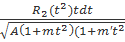Але другий підстановкою u= зразу приводиться до елементарного інтегралу
∫ 
і береться у кінцевому вигляді. Таким чином, наступним дослідженням належить лише інтеграл
∫ 
. (7)
Дата добавления: 2015-09-11; просмотров: 83 | Поможем написать вашу работу | Нарушение авторских прав |