Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Еліптичні інтеграли 1- го, 2- го та 3- го роду

Розглянемо елементарні із інтегралів виду (8), до яких могли б бути зведені усі інтеграли цього виду, тобто, і взагалі усі еліптичні інтеграли.

Виділимо із раціональної функції R(x), яка фігурує у підінтегральному виразі (8), цілу частину P(x), а правильно- дробову її частину розкладемо на прості дроби. Якщо не об'єднувати спряжені комплексні корені знаменника, а розглядати їх окремо, подібно раціональним кореням, R(x) матиме вигляд суми ступенів ( і дробів виду ( де a може бути і уявним числом, помножених на числовий коефіцієнт. Звідси зрозуміло, що інтеграл (8), у загальному випадку, є лінійним агрегатом наступних інтегралів

(

Зупинимося на інтегралах . Якщо проінтегрувати тотжність

=(2n-3) + = ,

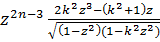то отримаємо рекурентне співвідношення

(2n-1) -(2n-2)( +(2n-3) = , (9)

яке пов'язує три послідовних інтеграла I.α

Нехай n=2, виразимо через і ;

якщо обрати n=3 і замість підставимо його вираження через і , то і буде виражатися через ці інтеграли. Продовжуючи цей процес, ми переконаємося, що кожен із інтегралів (n 2) буде виражатися через і , і навіть враховуючи (9), можна встановитиі вид пов'язуючої їх формули
= + + (z) ,
де і - сталі, а (z)- непарний многочлен ступеня 2n-3. Звідси зрозуміло, що якщо - многочлен n- ступеня від , то
∫ = + +z , (10)
де α і β- сталі, а - деякий многочлен (n-2)-ого ступеня від . Визначення цих сталих і коефіціентів многочлена (якщо многочлен конкретно заданий методом невизначених коефіціентів).
Зауважимо, що з (9) можна було б виразити через і інтеграл і при від'ємних значеннях (n=-1,-2,…), так що в інтегралах достатньо обмежитися випадком a 0.
Переходячи до інтегралів (наприклад, при дійсних a), подібним чином встановимо для них рекурентне співвідношення
(2m-2)[-a+( + +(2m-4)[()-3 , вірне і при від'ємних і нульовому значеннях m. Звідси усі можна виразити через три з них
=∫
∫ ,
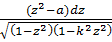= ∫ = -a ,
тобто остаточно через .
Зауважимо, що все це є справедливим і при уявних значеннях параметру a.
Отже: усі еліптичні інтеграли за допомогою елементарних підстановок- і з точністю до доданків, які виражаються у кінцевому вигляді,- приводяться до наступних трьох стандартних інтегралів:
(0

(останній отримаємо із , ввівши, замість a 0, новий параметр h=- ). Ці інтеграли, як показав Ліувілль, у кінцевому вигляді всж не беруться. Їх Лежандр назвав еліптичними інтегралами, відповідно, 1- го, 2- го і 3- го роду. Перші два містять лише один параметр k, а останній, крім нього, ще (комплексний) параметр h.
Лежандр вніс в ці інтеграли ще подальші спрощення, зробивши в них підстановку z=sin φ (φ змінюється від 0 до ).
При цьому перший з них беспосередньо переходить в інтеграл
. (11)
Другий перетворюється так:
= - ,

Тобто приводиться до попереднього інтеграла і до нового інтеграла
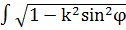
. (12)
Нарешті, третій інтеграл при вказаній підстановкі переходить в
. (13)
Інтеграли (11), (12) і (13) також називають еліптичними інтегралами 1- го, 2- го, та 3- го роду- у формі Лежандра.
З них більш важливі та частіше застосовні перші два. Якщо вважати, що ці інтеграли при звертаються в нуль і тим фіксувати довільні сталі, які містяться в них, то отримаємо досить визначені функції від , які Лежандр позначив відповідно через F(k, )та E(k, . Тут окрім незалежної змінної , вказаний також параметр k, яких називається модулем, який входить до виразу цих функцій.
Лежандром були складені обширні таблиці значення цих функцій при будь- яких і будь- яких k. В них не тільки аргумент , який трактується як кут, виражається у градусах, а і модуль k розглядається як синус деякого кута ϴ, який і вказується в таблиці замість модуля, і при тому також у градусах.
Окрім того, як Лежандром, так і іншими вченими були вивчені найглибші властивості цих функцій, було встановлено ряд формул, які стосуються їх і т.д. завдяки цьому функції F іE Лежандра увійшли до сім'ї функцій, які зустрічаються в аналізі і його додатках, на рівних правах із елементарними функціями.
нижча частина інтегрального числення займається «інтегруванням у кінцевому вигляді». Проте, було б помилковим вважати, що цим обмежуються завдання інтегрального числення взагалі: еліптичні інтеграли F та E є прикладами таких функцій, які плідно вивчаються за їх інтегральними виразами і з успіхом застосовуються, хоча і не можуть бути представлені через елементарні функції у кінцевому вигляді.