Читайте также:
|
Покажемо, що кожен інтеграл типу (7) може бути представленим у формі
∫ 
, (8)
де k це деякий правильний дріб: 0<k<1.
Назвемо цю форму канонічною.
Нехай для кратності y= 
.
Не зменшуючи загальності, можемо вважати тут A= 
1; крім того, для визначеності обмежимося додатнім значенням t. Розглянемо тепер різні можливі комбінації знаків А, m, 
і вкажемо підстановку для кожного випадку, яка приведе інтеграл (7) до канонічної форми.
1) А=+1, m=- 
, =- 
(h 
). Для того, аби радикал мав дійсні значення, необхідно, аби бул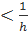о t 
або t 
. Нехай
ht=z, де 0 
або z 
.
Тоді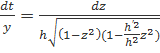 
, так що за k тут варто прийняти 
.
2) А=+1, m=- , = (h 
). Для того, аби радикал мав дійсні значення, обмежимося значенням t .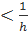
Нехай ht= 
, де 0 
.
Тоді 
.
можна взяти k= 
.
3) А=+1, m= , = 
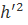(h 
). Зміна tнічим не обмежена. Нехай
ht= 
, де 0 
z 
1.
У цьому випадку 
і k= 
.
4) А=-1, m=- , 
= 
(h 
). Зміна t обмежена нерівністю t 
.
Нехай ht= 
, де 0 ,
так що 
і k= 
.
5) А=-1, m=- , =- (h ).
Змінна t може змінюватися лише між 
та 
.
Нехай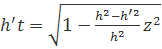 
, де 0 .
Маємо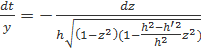 
і k= .
Цим вичерпуються усі можливі випадки, адже у випадку, коли А=-1 і обидва числа m, 
0, радикал взагалі не може мати дійсних значень. Про множник 
(
) ми не говорили нічого, адже в усіх інших випадках він, в очевидь, перетворювався у раціональну функцію від 
Зауважимо, що розглядаючи інтеграл (8), ми можемо обмежитися значеннями z 
1; випадок z 
зводиться до цього підстановкою kz= 
, де 
.
Дата добавления: 2015-09-11; просмотров: 82 | Поможем написать вашу работу | Нарушение авторских прав |