
Читайте также:
|
План
Вступ
1. Загальні означення
2. Допоміжні перетворення
3. Зведення до канонічної форми
4. Еліптичні інтеграли 1- го, 2- го та 3- го роду
5. Приклад. Інтеграли, які зводяться до еліптичних
Висновки
Література
Вступ
У багатьох питаннях науки і техніки доводиться не по заданій функції шукати її похідну, а навпаки – відновлювати функцію по відомій її похідній.
Дамо наступне означення:
Функція F(x) на даному проміжку називається первісною функцією для функції f(x) або інтегралом від f(x), якщо на всьому цьому проміжку f(x) являється похідною для функції F(x) або, що те ж саме, f(x)dx служить для F(x) диференціалом
F’(x)= f(x) або dF(x)= f(x)dx.
Пошук для функції всіх її первісних, що називається інтегруванням її, і складає одну з задач інтегрального числення; як бачимо, ця задача являється оберненою основній задачі диференціального числення. Так, наприклад, для обчислення довжини дуги еліпса чи деякої її частини необхідно розв’язати певні еліптичні інтеграли, яким і присвячена дана курсова робота.
У інтегральному численні еліпти́чний інтегра́л з'явився у зв'язку із завданням обчислення довжини дуги еліпса і був вперше досліджений Джуліо Фаніано і Леонардом Ейлером.
Загальні означення
Розглянемо інтеграл вигляду ∫ R(x, y)dx, (1)
де y- алгебраїчна функція від x, тобто вона задовольняє алгебраїчному рівнянню
P(x, y)=0 (2)
(P- цілий відносно x та y многочлен). Інтеграли такого роду отримали назву абелевих інтегралів.
∫ R(x, 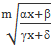 )dx, ∫R(x,
)dx, ∫R(x, 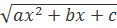 )dx.
)dx.
Дійсно, функції
y=  , y=
, y= 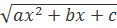
задовольняють, відповідно, алгебраїчним рівнянням
(γx+δ)  -(αx+β)=0,
-(αx+β)=0, 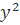 -(a
-(a  +bx+c)=0.
+bx+c)=0.
З геометричної точки зору, абелевий інтеграл (1) вважають пов'язаним з тією алгебраїчною кривою, яка визначена рівнянням (2). Наприклад, інтеграл
∫R(x, 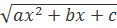 )dx (3)
)dx (3)
пов'язаний із кривою другого порядку 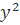 =a
=a  +bx+c.
+bx+c.
якщо крива (2) може бути представлена параметрично
x=  (t), y=
(t), y=  (t)
(t)
так, що функції  (t),
(t),  (t) виявляються раціональними, то в інтегралі (1) стає можливою раціоналізація підінтегрального виразу: підставкою x=
(t) виявляються раціональними, то в інтегралі (1) стає можливою раціоналізація підінтегрального виразу: підставкою x=  (t) воно приводиться до вигляду
(t) воно приводиться до вигляду
R( (t),
(t),  (t)),
(t)), 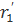 (t)dt.
(t)dt.
До цього класу і відносяться обидва згадані вище випадки. Таким чином можлива раціоналізація підінтегрального виразу в інтегралі типу (3) пов'язана саме з тим фактом, що крива другого порядку унікурсальна.
Очевидно, що змінні x та t пов'язані алгебраїчним рівнянням, так що t є алгебраїчною функцією від x. Якщо розширити клас елементарних функцій, включивши в нього і усі алгебраїчні функції, то можна сказати, що у випадку унікурсальності кривої (2), інтеграл (1) завжди виражається через елементарні функції у кінцевому вигляді.
Однак подібна обставина є у деякому сенсі виключенням. У загальному випадку крива (2) не унікурсальна, а тоді, як можна довести, інтеграл (1) свідомо не завжди, тобто не при будь- якій функції R, може бути вираженим у кінцевому вигляді.
Із цим ми вже мали справу при розгляданні важливого класу інтегралів
∫R(x, 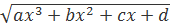 )dx,
)dx,
∫R(x, 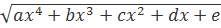 )dx, (4)
)dx, (4)
які містять квадратний корінь із многочленів 3- го та 4- го ступеня. Інтеграли вигляду (4)- як правило- вже не виражаються у кінцевому вигляді через елементарні функції навіть у розширеному розумінні цього терміна.
Многочлени під коренем в (4) припускаються такими, що мають дійсні коефіцієнти. Крім того, ми завжди будемо вважати, що у них немає кратних коренів, інакше було б можливо винести лінійний множник з- під знака кореня; питання звелося б до інтегрування виразів вже раніше вивчених типів, і інтеграл виразився би у кінцевому вигляді. Остання обставина може мати місце і при відсутності кратних коренів; наприклад, легко перевірити, що
∫  =
=  +c,
+c,
∫  dx=x
dx=x 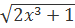 +c.
+c.
Інтеграли типу (4) називають еліптичними.
Дата добавления: 2015-09-11; просмотров: 86 | Поможем написать вашу работу | Нарушение авторских прав |