Читайте также:
|
Генератор поля Галуа с примитивным многочленом степени n в цепи обратной связи является счетчиком, имеющим pn-1 состояний (если p=2, то 2n-1).
На рис.39 приведена схема счетчика с числом состояний 25-1.
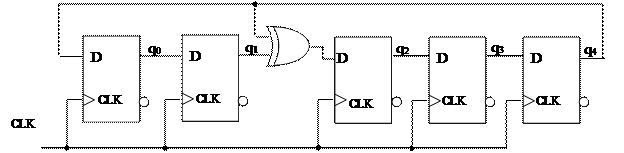
Рис. 39.
Примитивным многочленом и делителем многочлена x31-1 является многочлен
d(x) = 1+x2+x5, включенный в цепь обратной связи.
Единице, сдвигаемой из старшего разряда, соответствует элемент a5. Обратная связь заменяет его на равный ему элемент 1+a2.
Это следует из того, что a является корнем d(x), т.е. 1+ a2 + a5 =0. Отсюда следует, что a5 = 1+a2.
Каждому внутреннему многочлену ЛПМ ставится в соответствие вектор (q0,q1,... qn-1), где q0,q1,... qn-1 - коэффициенты при соответствующих степенях a (qi – выход i-й задержки).
Тогда последовательность состояний счетчика будет следующей:
(q0 q1 q2 q3 q4)
S0 a0 = 1 1 0 0 0 0
S1 a1 = a 0 1 0 0 0
S2 a2 = a2 0 0 1 0 0
S3 a3 = a3 0 0 0 1 0
S4 a4 = a4 0 0 0 0 1
S5 a5 = 1 + a2 1 0 1 0 0
S6 a6 = a + a3 0 1 0 1 0
S7 a7 = a2 + a4 0 0 1 0 1
S8 a8 = 1 + a2 + a3 1 0 1 1 0
.
.
.
S30 a30 = a + a4 0 1 0 0 1
a31 = a0 =1.
LFSR-счетчик никогда не проходит в цикле через состояние 0000. Это состояние является состоянием покоя.
Достоинством полиномиальных счетчиков является то, что сложность комбинационной схемы не зависит от числа разрядов счетчика, а определяется выражением для многочлена, включенного в цепь обратной связи. В случае параллельного двоичного счетчика функция возбуждения старшего разряда зависит от n-1 переменных состояния. Например, для построения счетчика с числом разрядов n=10 и примитивным многочленом в цепи обратной связи 1+x7+x10 требуется всего oдин двухвходовой элемент XOR.
Недостатком, по сравнению с двоичными счетчиками, является то, что необходима перекодировка содержимого счетчика в двоичный код.
Рассмотренные схемы полиномиальных счетчиков называют сдвигающими регистрами с линейной обратной связью (LFSR – linear feedback shift-register), которые используются, в основном, в качестве генераторов псевдослучайных чисел и в ряде других случаев.
Линейным сдвигающим регистром является регистр, который построен только на D-триггерах и схемах “исключающее ИЛИ (сумма по mod 2)”. Функции возбуждения всех триггеров линейны.
4.5. Фибоначчи LFSR (Fibonacci LFSR (n=5))
Другой разновидностью LFSR является Фибоначи LFSR (рис.40).
 |
Рис.40
d(x) = 1+x2+x 5
Последовательность состояний, генерируемых данной схемой, отличается от последовательности состояний LFSR Галуа.
Некоторые полиномы, принадлежащие максимальному показателю
Таб.16
| N | Feedback polynomial | Period (2n -1) |
| x2 + x +1 | ||
| x3 + x +1, x3 + x2 +1 | ||
| x4 + x3 +1, x4 + x +1 | ||
| x5 + x3 +1, x5 + x2 +1 | ||
| x6 + x5 +1, x6 + x +1 | ||
| x8+ x6 + x5 +x4 + 1 | ||
| x9 + x5 +1, x9 + x4 +1 | ||
| x10 + x7 +1 | ||
| x11 + x9 +1, x11 + x2 +1 | ||
| x12+ x11 + x10 +x4 + 1 | ||
| x13+ x12 + x11 +x8 + 1 |
4.6. 
Примеры 3-разрядных LFSR с полиномом d(x) = 1 + x2 + x3
Galois LFSR Рис. 41
Полином d(x) = 1 + x2 + x3 принадлежит максимальному показателю М=23 – 1.
Схема генерирует все 7 полиномов по модулю неприводимого полинома d(x) = 1 + x2 + x3.
Поэтому данная схема имеет 7 состояний. Эти состояния указаны в таблице 16.
D(a) =0. 1+a2 + a3 =0; a3 = 1+a2
Taб.16
| State | Polynomials | q0 q1 q2 | |
| S0 | a0 | 1 0 0 | |
| S1 | a1 | a | 0 1 0 |
| S2 | a2 | a2 | 0 0 1 |
| S3 | a3 | 1 + a2 | 1 0 1 |
| S4 | a4 | 1 + a + a2 | 1 1 1 |
| S5 | a5 | 1 + a | 1 1 0 |
| S7 | a6 | a + a2 | 0 1 1 |
| S8 =S0 | a7 | 1 0 0 |
Fibonacci LFSR
Рис.42
Последовательность состояний счетчика представлена в Таб. 17.
Таб.17
| State | q2 q1 q0 |
| S0 | 1 0 0 |
| S1 | 1 1 0 |
| S2 | 1 1 1 |
| S3 | 0 1 1 |
| S4 | 1 0 1 |
| S5 | 0 1 0 |
| S7 | 0 0 1 |
| S8 =S0 | 1 0 0 |
Последовательность состояний отличается от последовательности состояний генератора элементов поля Галуа.
4.7. Примеры 8-миразрядных LFSR с d(x) =1+ x4 + x5 + x6 + x8
1. Galois LFSR Рис. 43
2. Fibonacci LFSR Рис. 44
Дата добавления: 2015-09-11; просмотров: 151 | Поможем написать вашу работу | Нарушение авторских прав |