Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Представление перестановок в циклической форме.

Во многих приложениях удобно представлять перестановки в циклической форме.

Пример. Разложение перестановки на циклы.

Пусть f=<5 7 3 1 6 4 2>= , тогда эту перестановку можно записать так

2à7

Каждый цикл выписан на отдельной строчке. Внутри цикла следующим выписывается элемент перестановки, являющийся образом в f текущего, т. е. xàf(x). Образ последнего элемента совпадает с первым. В этом примере первым в каждом цикле выписан элемент с наименьшим номером внутри цикла, a циклы расположены в порядке возрастания первых элементов

Рассмотрим некоторые свойства разложений на циклы и введем дополнительные обозначения.

Пусть перестановка f содержит k циклов следующего вида:

, для i=1,...,k,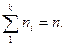

Каждому такому циклу соответствует перестановка f_i = [ ], называемая также циклом длины n_i, которая определяется следующим образом:

f_i()= ,...,f_i()= ; f_i(x)=x для xÏ { }.

Перестановку f можно представить в виде суперпозиции циклов

f = .

Например, f = <7 5 1 4 2 3 6>, тогда f = [1,7,6,3]×[2,5]×[4].

Замечание. 1. Элементы внутри одного цикла можно циклически переставлять местами.

Например: [1,7,6,3]=[7,6,3,1]=[6,3,1,7]=[3,1,7,6].

Теорема 1. Общее число циклов во всех n! перестановках

n-го порядка равно n!´H_n, где H_n= .

Доказательство. Пусть все n! перестановок записаны в циклической форме. Зафиксируем i, 1£i£n, и рассмотрим, сколько циклов длины i встречается во всех этих перестановках.

Заметим, что конкретный цикл [a₁,...,a_i] встречается в (n-i)! перестановках, так как это число способов, которыми можно переставить оставшиеся n-i элементов. Число различных возможных циклов [a₁,...,a_i] есть n´(n-1)´¼´(n-i)/i, так как элемент a₁ можно выбрать n способами, элемента a₂ - (n-1) способами и т. д.; а среди n´(n-1)´¼´(n-i+1) циклов из a₁,...,a_i фиксированных элементов появляется i раз, как [а₁,...,а_i], [a₂,...,a_i,a₁],...,[a_i,a₁,...,a_i-1]. Поэтому общее число циклов из i элементов во всех n! перестановках есть n´(n-1)´¼´(n-i+1)/i, взятое (n-i)! раз, т. е. n!/i.

Суммируя по всем i, получаем общее число циклов во всех n! перестановках =n!´H_n.

Определение. Будем говорить, что перестановка, представленная в виде разложения на циклы, находится в канонической форме, если:

а) обязательно записываются все циклы;

б) в каждом цикле первым записывается элемент с наименьшим значением;

в) циклы располагаются в порядке убывания значений первых элементов.

Например, f=[3 1 6 7]×[5 4] представляется как [4 5]×[2]×[1 6 7 3].

Скобочная структура в канонической форме может быть опущена, так как первым элементам циклов соответствуют левосторонние минимумы (a_k, i£k£n, является левосторонним минимумом f, если a_k<a_i, 1£i<k).

В приведенном примере перестановка f может быть записана как (4 5 2 1 6 7 3), где круглые скобки указывают, что перестановка представлена в канонической циклической форме.

Упражнение. Пусть f=<a₁... a_n>, g=(a₁... a_n),n¹1. Докажите, что f¹g.

Рассмотрим производящую функцию С_n(t)= , определяющую число перестановок n-го порядка, имеющих k циклов, т. е. С(n,k) определяет число перестановок n-го порядка, имеющих k циклов. Тогда

C(0,0)=1,

C(n,0)=0, при n>0,

C(n,k)=0, при к>n,

Для n>0, C(n,k)=С(n-1,k-1)+(n-1)C(n-1,k) или C_n(t)=(t+n-1)C_n-1(t).

Докажем последнее утверждение.

Все ниже рассматриваемые перестановки представлены в канонической циклической форме. Заметим, что если максимальное число в такой перестановке расположено на первом месте, то оно образует отдельный цикл (так как оно является левосторонним минимумом и следующее за ним число также левосторонний минимум). Если же оно расположено на любом другом месте, то оно входит в какой-то цикл длины, большей единицы. Перестановка n-го порядка, содержащая k циклов, может быть получена либо добавлением n на первое место в перестановку (n-1)-го порядка, содержащую k-1 цикл, либо добавлением n в перестановку(n-1)-го порядка, содержащую k циклов, на любое место со второго до n-го.

Следствие. Учитывая, что C₁(t)=t, получаем

C_n(t)=t(t+1)…(t+n-1).