Читайте также:
|
В случае коммутативных алгебраических операций произведения х1х2 и х2х1 одинаковы. Поэтому производящую функцию, описывающую перестановки, невозможно построить так, как это было сделано для сочетаний. В случае n различных элементов из соотношения p(n,m)=”число m-перестановок” вытекает, что (1+t)n =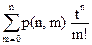 
, т. е. в разложении выражения (1+t)n число p(n,m) является коэффициентом при 
. Этот факт указывает пути обобщения.
Если какой-либо элемент может появляться 0,1,…,k раз или если существует k элементов данного вида, то множитель 1+t в левой части равенства заменяется множителем 1+t+ 
+…+ 
. Это объясняется тем, что число перестановок из n элементов, p из которых одного вида, q другого и т. д., равно
.
Это число оказывается коэффициентом при в произведении
× 
× × ×, n=p+q+…,
что в точности соответствует необходимым требованиям.
Определение и простейшие свойства производящих функций. [1]
Определение. Обычной производящей функцией для последовательности a0,a1,… называется формальная сумма
A(t)=a0+a1t+a2t2+ … antn+…. (1)
Экспоненциальной производящей функцией для той же последовательности называется сумма
Е(t)=a0+a1t+a2t2/2!+ … antn/n!+…. (2)
В связи с этими определениями необходимо сделать несколько замечаний. Во-первых, элементы последовательности a0,a1,…, как видно, из самих обозначений, упорядочены, но не обязательно должны быть различны. Во-вторых, переменная t производящей функции никак не определена.
На производящих функциях можно определить формальные операции, такие как сложение, умножение, дифференцирование и интегрирование по t, и выявить зависимости в этой алгебре, в частности путем приравнивания коэффициентов при степенях tn после выполнения этих операций. С этой точки зрения неуместно ставить вопрос о сходимости соответствующих рядов.
Алгебра степенных рядов A(t), определяющих производящие функции, известна под именем алгебры Коши, а алгебра степенных рядов E(t), определяющих экспоненциальные производящие функции, известна как символическое исчисление Блиссара. В статистике функция E(t) фигурирует как производящая функция моментов; E(t) используется также в теории чисел.
В комбинаторике неизбежно возникают производящие функции, отличные от А(t) или E(t), например, сумма вида
G(t)= a0f0(t)+a1f1(t)+a2f2(t)+ … anfn(t)+…, (*)
для которой единственным требованием является линейная независимость функций f0(t), f1(t),…(для того чтобы сделать выражение однозначным). A(t) и E(t) являются частными случаями этого выражения.
Наконец, для любителей операций над непрерывными переменными следует отметить, что аналогом обычной производящей функции с одной переменной служит несобственный интеграл
А(t)= 
Этот факт, по-видимому, более известен для случая экспоненциального ядра е-tk, т. е. для преобразования Лапласа
А(t)= 
Выражение, включающее в себя как частные случаи оба приведенные выше интеграла и степенные ряды, представляет собой интеграл Стильтьеса
А(t)= 
,
в котором t – параметр. Чтобы получить сумму (1), в качестве функции F(t,k) выбираем ступенчатую функцию. Эта функция имеет скачки при к=0,1,2,…; скачок в точке k равен tk.
Некоторые простейшие производящие функции.
| ak | A(t) | E(t) |
| ak | (1-at)-1 | Exp at |
| k | t(1-t) | t exp t |
| k(k-1) | 2t2(1-t)-3 | t2 exp t |
| k2 | t(t+1)(1-t)-3 | t(t+1) exp t |
c 
| (1+t)n | - |
| n(n-1)…(n-k+1) | - | (1+t)n |
Упражнение. Докажите справедливость приведенных формул.
Элементарные соотношения между обычными производящими функциями.
Обозначим через A(t), B(t), C(t) производящие функции, соответствующие последовательностям (ак), (bк), (cк), тогда в качестве непосредственного следствия из самого определения последовательности (а) получаем две пары соотношений; в каждой паре выполнение одного из соотношений влечет за собой выполнение второго
Сумма ак=bк+cк
A(t)=B(t)+C(t)
Произведение ак=bкc0+bк-1c1+…+b1cк-1+b0cк
A(t)=B(t)×C(t)
Последовательность (ак) называется сверткой (bк) и (cк), если A(t)=B(t)×C(t). Сумма и произведение обладают свойствами коммутативности и ассоциативности.
Для экспоненциальных производящих функций соответствующие соотношения определяются следующим образом:
Пусть E(t), F(t), G(t) экспоненциальные производящие функции, соответствующие последовательностям (eк), (fк), (gк), тогда
Сумма eк=fк+gк
E(t)=F(t)+G(t)
Произведение eк= 
fкg0+ 
fк-1g1+…+ 
f1gк-1+ 
f0gк
E(t)=F(t)×G(t)
Дата добавления: 2015-09-11; просмотров: 87 | Поможем написать вашу работу | Нарушение авторских прав |