
Читайте также:
|
(Лекции 2004, фрагменты)
Санкт-Петербург
09.05.2004
Докажем, что число счастливых 2n-значных трамвайных билетов равно
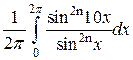 .
.
Билет считается счастливым, если сумма первых n цифр его номера равна сумме n последних цифр, например, билет с номером 764395 – счастливый шестизначный билет.
Упражнение. Докажите, что функция от параметра n, вычисляющая число счастливых 2n-значных трамвайных билетов, примитивно рекурсивна.
Доказательство (леммы).
Рассмотрим равенство (1+z+…+z9)n=  , тогда аi определяет количество n-значных чисел, сумма цифр которых равна i.
, тогда аi определяет количество n-значных чисел, сумма цифр которых равна i.
Нам нужно вычислить  .
.
Имеем (1+z+…+z9)n(1+z-1+…+z-9)n= 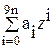 ´
´ 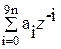 =
=  ,
,
тогда b0=  .
.
(1+z+…+z9)n(1+z-1+…+z-9)n= 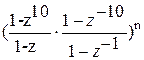 =
=  .
.
Известно, что  =
=  .
.
Пусть z=eij=cosj+isinj, тогда b0=  =
= 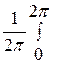
 =
= 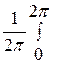
 .
.
Преобразуем  =
=
 =
=
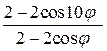 =
=  =
=  .
.
Таким образом,
b0=  =
= 
 =
= 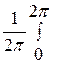
 .
.
При доказательстве тех или иных комбинаторных тождеств часто используется одно или одновременно два из следующих правил:
Правило суммы. Если объект А может быть выбран m способами, а объект В другими n способами, то выбор “либо А, либо В” может быть осуществлен m+n способами.
Правило произведения. Если объект А может быть выбран m способами и после каждого из таких выборов объект В в свою очередь может быть выбран n способами, то выбор “А, и В” в указанном порядке может быть осуществлен m×n способами.
Примеры. На основе этих правил в курсе математического анализа легко были получены формулы для числа k-перестановок  и числа k-сочетаний
и числа k-сочетаний  из n объектов, а именно
из n объектов, а именно
 = n(n-1)…(n-k+1)
= n(n-1)…(n-k+1)
 =
= 
Упражнение. Докажите, что число k-перестановок из n объектов с повторениями равно nk.
Задача. Доказать, что число k-сочетаний из n объектов с повторениями равно 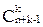 .
.
Решение (Л. Эйлер): Пусть X={1,2,…n} и рассмотрим любое из k-сочетаний с повторениями с1с2…сk этих n чисел (считаем, что в сочетании с1с2…сk элементы выписаны в неубывающем порядке). Естественно, что в каждом сочетании вследствие возможности неограниченных повторений любые рядом стоящие элементы могут быть одинаковыми. Ввиду этого обстоятельства строим с помощью соотношений
d1=c1+0; d2=c2+1;…; di=ci+i-1;…; dk=ck+k-1
последовательность элементов d1d2…dk следовательно, при любых элементах ci элементы di всегда различны. Ясно, что отображение с1с2…сk в d1d2…dk биективно. Число последовательностей из элементов di равно числу k-сочетаний без повторений из элементов от 1 до n+k-1, т. е. 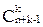 .
.
Дата добавления: 2015-09-11; просмотров: 119 | Поможем написать вашу работу | Нарушение авторских прав |
|