Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

ЧАСТИНА ІІ

ТЕСТОВІ ЗАВДАННЯ

З КУРСУ „ТЕХНІЧНА МЕХАНІКА”

ЧАСТИНА ІІ

№ з/п	Питання	Відповіді
	1.		Якою може бути найбільша вага тіла 2, щоби тіло 1 вагою 200 Н залишалось нерухомим? Коефіцієнт тертя ковзання f = 0,2, блок О ідеальний.	а)	40 Н;
	б)	50 Н
	в)	20 Н
	г)	100 Н
	д)	200 Н
	2.		Тіло 1 вагою 500 Н і тіло 2 вагою 100 Н рухаються рівномірно відповідно горизонтально і вертикально. Чому дорівнює коефіцієнт тертя ковзання f, якщо шарнір О ідеальний?	а)	1,0
	б)	5,0
	в)	0,5
	г)	0,1
	д)	0,2
	3.		Яке мінімальне значення маси m 2 тіла 2 при якому тіло 1 з масою m 1 залишається нерухомим. Коефіцієнт тертя ковзання дорівнює f. Блок О ідеальний.	а)	m 1 (cos 60° - f sin 60°)
	б)	m 1 (cos 60° + f sin 60°)
	в)	m 1 (sin 60° + f cos 60°)
	г)	m 1 (cos 60° - f sin 60°)
	д)	m 1 (f sin 60°- f cos 60°)
	4.		Яке максимальне значення маси m 2 тіла 2 при якому тіло 1 з масою m 1 залишається нерухомим? Коефіцієнт тертя ковзання дорівнює f. Блок О ідеальний.	m 2 =
	а)	m 1 (cos 60° - f sin 60°)
	б)	m 1 (sin 60° - f cos 60°)
	в)	m 1 (sin 60° + f cos 60°)
	г)	m 1 (cos 60° + f sin 60°)
	д)	m 1 (f sin 60°- cos 60°)
	5.		Яким може бути максимальне значення сили при якому тіло з масою m залишається нерухомим? Кут нахилу a, коефіцієнт тертя ковзання дорівнює f.	F =
	а)	mg f ( sin a + cos a)
	б)	mg ( sin a - f cos a)
	в)	mg ( sin a + f cos a)
	г)	mg ( cos a - f sin a)
	д)	mg ( cos a - f sin a)
6.		Яке максимальне значення маси m 2 тіла 2 при якому тіло 1 з масою m 1 залишається нерухомим? Коефіцієнт тертя ковзання дорівнює f. Блок О ідеальний.	m 2 =
а)	m 1 (cos 60° - f sin 60°)
б)	m 1 (sin 60° - f cos 60°)
в)	m 1 (sin 60° + f cos 60°)
г)	m 1 (cos 60° + f sin 60°)
д)	m 1 (f sin 60°- cos 60°)
7.		Яким може бути максимальне значення сили при якому тіло з масою m залишається нерухомим? Кут нахилу a, коефіцієнт тертя ковзання дорівнює f.	F =
а)	mg f ( sin a + cos a)
б)	mg ( sin a - f cos a)
в)	mg ( sin a + f cos a)
г)	mg ( cos a - f sin a)
д)	mg ( cos a - f sin a)
8.		Якою може бути найбільша вага тіла 2, щоби тіло 1 вагою 200 Н залишалось нерухомим? Коефіцієнт тертя ковзання f = 0,2, блок О ідеальний.	а)	40 Н;
б)	50 Н
в)	20 Н
г)	100 Н
д)	200 Н
	9.		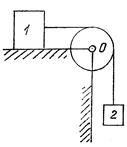Тіло 1 вагою 500 Н і тіло 2 вагою 100 Н рухаються рівномірно відповідно горизонтально і вертикально. Чому дорівнює коефіцієнт тертя ковзання f, якщо шарнір О ідеальний?	а)	1,0
	б)	5,0
	в)	0,5
	г)	0,1
	д)	0,2
	10.		Яке мінімальне значення маси m 2 тіла 2 при якому тіло 1 з масою m 1 залишається нерухомим. Коефіцієнт тертя ковзання дорівнює f. Блок О ідеальний.	а)	m 1 (cos 60° - f sin 60°)
	б)	m 1 (cos 60° + f sin 60°)
	в)	m 1 (sin 60° + f cos 60°)
	г)	m 1 (cos 60° - f sin 60°)
	д)	m 1 (f sin 60°- f cos 60°)

№ з/п	Питання	Відповіді
	11.		Драбина АВ вагою G =100 Н, стоїть на підлозі з коефіцієнтом тертя f =0,25, а в точці А опирається на ідеально гладку стіну. Чому дорівнює сила тертя, яка утримує драбину в рівновазі?	а)	50 Н
	б)	75 Н
	в)	0 Н
	г)	25 Н
	д)	125 Н
	12.		Яку найменшу силу Р потрібно прикласти до гальмівної колодки В, щоб утримати вантаж G =200 Н. Відомо, що коефіцієнт тертя між колодкою та барабаном f =0,2.	а)	200 Н
	б)	2000 Н
	в)	40 Н
	г)	1000 Н
	д)	400 Н
13.		Яку найменшу силу Р потрібно прикласти до гальмівної колодки В, щоб утримати вантаж G =400 Н. Відомо, що коефіцієнт тертя між колодкою та барабаном f =0,2, а r =0,1 м, R =0,15 м	а)	1333,33 Н
б)	133,33 Н
в)	209,2 Н
г)	340,57 Н
д)	635,2 Н

14.		Прямокутний брус А вагою Р =100Н, знаходиться в стані рівноваги на похилій площині з кутом нахилу =30°. Коефіцієнт тертя між площиною та брусом f =0,577. Чому дорівнює сила тертя, яка утримує брус?	а)	50 Н
б)	59,7 Н
в)	28,85 Н
г)	25 Н
д)	33,33 Н
15.		Сила прижиму гальмівної колодки F =200 Н. Радіус гальмівного барабану R =0,1м, а коефіцієнт тертя між колодкою та барабаном f =0,4. Чому дорівнює максимальна вага вантажу Р, яка може утримуватись цим гальмом?	а)	200 Н
б)	100 Н
в)	400 Н
г)	2000 Н
д)	80 Н

16.		Прямокутний брус А вагою Р =10Н, знаходиться в стані рівноваги на похилій площині з кутом нахилу =30°. Коефіцієнт тертя між площиною та брусом f =0,577. Чому дорівнює сила тертя, яка утримує брус?	а)	5,0 Н
б)	5,97 Н
в)	2,88 Н
г)	2,5 Н
д)	3,33 Н

17. 1		Яку найменшу силу Р потрібно прикласти до гальмівної колодки В, щоб утримати вантаж G =400 Н. Відомо, що коефіцієнт тертя між колодкою та барабаном f =0,2, а r =0,1 м, R =0,15 м	а)	1333,33 Н
б)	133,33 Н
в)	209,2 Н
г)	340,57 Н
д)	635,2 Н
18. 2		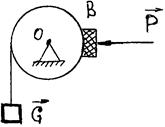Яку найменшу силу Р потрібно прикласти до гальмівної колодки В, щоб утримати вантаж G =200 Н. Відомо, що коефіцієнт тертя між колодкою та барабаном f =0,2.	а)	200 Н
б)	2000 Н
в)	40 Н
г)	1000 Н
д)	400 Н

19. 3		Драбина АВ вагою G =100 Н, стоїть на підлозі з коефіцієнтом тертя f =0,25, а в точці А опирається на ідеально гладку стіну. Чому дорівнює сила тертя, яка утримує драбину в рівновазі?	а)	50 Н
б)	75 Н
в)	0 Н
г)	25 Н
д)	125 Н
20. 4		Яку найменшу силу Р потрібно прикласти до гальмівної колодки В, щоб утримати вантаж G =100 Н. Відомо, що коефіцієнт тертя між колодкою та барабаном f =0,2.	а)	100 Н
б)	1000 Н
в)	20 Н
г)	500 Н
д)	200 Н