Студопедия
Главная страница | Контакты | Случайная страница

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Разложение в ряд Тэйлора, разностные аналоги производных

Читайте также:
  1. II. Характерное ортогональное разложение
  2. Аналогичным способом вяжутся петли с перекрещиванием влево.
  3. Аналогия скороварки
  4. ВИТАМИНЫ И ИХ АНАЛОГИ
  5. Галогено- та гидроксипохідні вуглеводнів та їх тіоаналоги
  6. Глава 3. Разложение остатков общинно-родовых отношений в Швеции
  7. Дедукция и аналогии
  8. Ж) Смысл аналогий
  9. За десять месяцев-2012 украинский железорудный экспорт увеличился на 4,4% в сравнении с аналогичным периодом прошлого года
  10. зависящие от производных высшего порядка нескольких функции

 

 

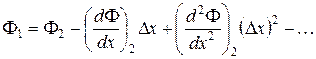
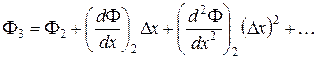
Отбрасывая все члены порядка выше (D x)2 и вычитая Ф1 из Ф3 получим уравнение для первой производной,

а складывая – для второй

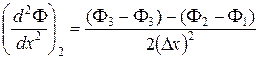(3.1)

· аппроксимация, порядок аппроксимации

аппроксимирует I производную со II порядком, (3.2)

аппроксимирует I производную с I порядком. (3.3)

· чем больше точек, тем точнее дискретный аналог описывает исходное ДУ; на грубых сетках результаты будут хуже.

Результаты решения ОДУ с применением схем I и II порядков

 

Как влияет шаг сетки на результат численного решения

           
0.1 1.1 0.004679      
0.2 1.21 0.009336 0.2 1.2 0.017523
0.3 1.331 0.013971      
0.4 1.4641 0.018584 0.4 1.44 0.034739
0.5 1.61051 0.023176      
0.6 1.771561 0.027747 0.6 1.728 0.051653
0.7 1.948717 0.032296      
0.8 2.143589 0.036823 0.8 2.0736 0.068271
0.9 2.357948 0.04133      
  2.593742 0.045815   2.48832 0.084598

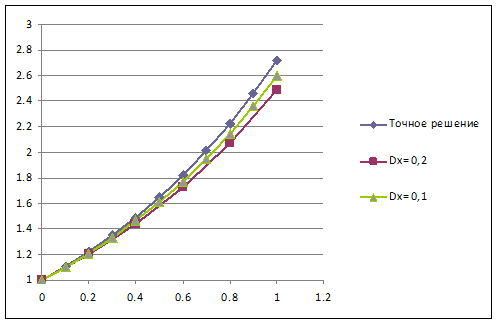
Как влияет порядок аппроксимации разностной схемы на результаты решения.

Правая разность   Центральная разность Точное решение
             
0.2 1.2 0.018 0.2 1.2 0.018 1.221403
0.4 1.44 0.035 0.4 1.48 0.0079 1.491825
0.6 1.728 0.052 0.6 1.792 0.017 1.822119
0.8 2.0736 0.068 0.8 2.1968 0.013 2.225541
  2.48832 0.085   2.67072 0.017 2.718282

 

 

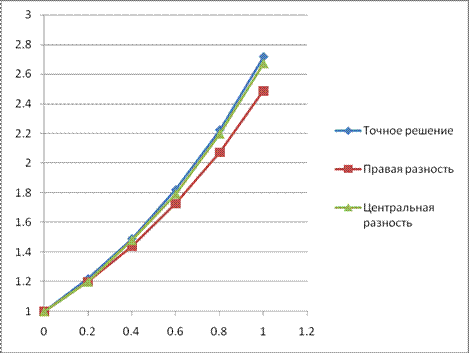
Вывод. Более высокий порядок аппроксимации позволяет получить более точное решение при меньшем числе узлов сетки.

 

Л.3

===================================

 

Устойчивость и консервативность разностных схем

 



Дата добавления: 2015-09-10; просмотров: 109 | Поможем написать вашу работу | Нарушение авторских прав
Введение в предмет изучения. | Как влияет число Куранта на устойчивость разностной схемы. | Консервативность разностных схем. |

lektsii.net - Лекции.Нет - 2014-2025 год. (0.006 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав