Читайте также:
|
Часто приходилось слышать мнение, что метод вариации произвольных постоянных для уравнения второго порядка – штука не из легких. Но я предполагаю следующее: скорее всего, метод многим кажется трудным, поскольку встречается не так часто. А в действительности особых сложностей нет – ход решения чёткий, прозрачный, понятный. И красивый.
Для освоения метода желательно уметь решать неоднородные уравнения второго порядка способом подбора частного решения по виду правой части. Данный способ подробно рассмотрен в статье Неоднородные ДУ 2-го порядка. Вспоминаем, что линейное неоднородное уравнение второго порядка с постоянными коэффициентами имеет вид:
Метод подбора, который рассматривался на вышеупомянутом уроке, проходит лишь в ограниченном ряде случаев, когда в правой части 
находятся многочлены, экспоненты, синусы, косинусы. Но что делать, когда справа, например, дробь, логарифм, тангенс? В такой ситуации на помощь как раз и приходит метод вариации постоянных.
Пример 4
Найти общее решение дифференциального уравнения второго порядка
Решение: В правой части данного уравнения находится дробь, поэтому сразу можно сказать, что метод подбора частного решения не прокатывает. Используем метод вариации произвольных постоянных.
Ничто не предвещает грозы, начало решения совершенно обычное:
Найдем общее решение соответствующего однородного уравнения:
Составим и решим характеристическое уравнение:
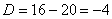
– получены сопряженные комплексные корни, поэтому общее решение: 
Обратите внимание на запись общего решения 
– если есть скобки, то их раскрываем.
Теперь проделываем практически тот же трюк, что и для уравнения первого порядка: варьируем константы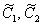 
, заменяя их неизвестными функциями 
. То есть, общее решение неоднородного уравнения будем искать в виде:
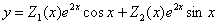, где – пока ещё неизвестные функции.
Далее необходимо решить систему двух уравнений с двумя неизвестными:
Похоже на свалку бытовых отходов, но сейчас всё рассортируем.
В качестве неизвестных выступают производные функций 
. Наша цель – найти производные , причем найденные производные должны удовлетворять и первому и второму уравнению системы.
Откуда берутся «игреки»? Их приносит аист. Смотрим на полученное ранее общее решение 
и записываем:
, 
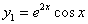Найдем производные:
С левыми частями разобрались. Что справа?
– это правая часть исходного уравнения, в данном случае: 
Коэффициент 
– это коэффициент при второй производной:
На практике почти всегда 
, и наш пример не исключение.
Всё прояснилось, теперь можно составить систему:
Систему обычно решают по формулам Крамера, используя стандартный алгоритм. Единственное отличие состоит в том, что вместо чисел у нас функции.
Найдем главный определитель системы:
Если позабылось, как раскрывается определитель «два на два», обратитесь к уроку Как вычислить определитель? Ссылка ведёт на доску позора =)
Итак: 
, значит, система имеет единственное решение.
Едем дальше:
Находим производную:
Но это еще не всё, пока мы нашли только производную.
Сама функция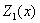 
восстанавливается интегрированием:
Здесь добавляем «нормальную» константу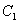 
Разбираемся со второй функцией:
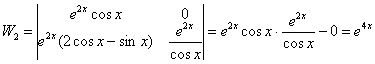
Здесь добавляем «нормальную» константу 
На заключительном этапе решения вспоминаем, в каком виде мы искали общее решение неоднородного уравнения? В таком:
Нужные функции только что найдены!
Осталось выполнить подстановку и записать ответ:
Ответ: общее решение: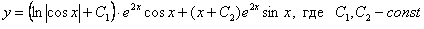 
В принципе, в ответе можно было раскрыть скобки.
Полная проверка ответа выполняется по стандартной схеме, которая рассматривалась на уроке Неоднородные ДУ 2-го порядка. Но проверка будет непростой, поскольку предстоит находить достаточно тяжелые производные и проводить громоздкую подстановку. Это неприятная особенность, когда вы решаете подобные диффуры.
Пример 5
Решить дифференциальное уравнение методом вариации произвольных постоянных
Это пример для самостоятельного решения. На самом деле в правой части тоже дробь. Вспоминаем тригонометрическую формулу 
, её, к слову, нужно будет применить по ходу решения.
Метод вариации произвольных постоянных – наиболее универсальный метод. Им можно решить любое уравнение, которое решается методом подбора частного решения по виду правой части. Возникает вопрос, а почему бы и там не использовать метод вариации произвольных постоянных? Ответ очевиден: подбор частного решения, который рассматривался на уроке Неоднородные уравнения второго порядка, значительно ускоряет решение и сокращает запись – никакого трахча с определителями и интегралами.
Рассмотрим два примера с задачей Коши.
Пример 6
Найти частное решение дифференциального уравнения, соответствующее заданным начальным условиям
, 
Решение: Опять дробь и экспонента в интересном месте.
Используем метод вариации произвольных постоянных.
Найдем общее решение соответствующего однородного уравнения:
– получены различные действительные корни, поэтому общее решение: 
Общее решение неоднородного уравнения ищем в виде: 
, где – пока ещё неизвестные функции.
Составим систему:
В данном случае:
, 
Находим производные:
, 
Таким образом:
Систему решим по формулам Крамера:
, значит, система имеет единственное решение.
Восстанавливаем функцию 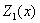интегрированием:
Здесь использован метод подведения функции под знак дифференциала.
Восстанавливаем вторую функцию интегрированием:
Такой интеграл решается методом замены переменной:
Из самой замены выражаем:
Таким образом:
Данный интеграл можно найти методом выделения полного квадрата, но в примерах с диффурами я предпочитаю раскладывать дробь методом неопределенных коэффициентов:
Обе функции найдены:
В результате, общее решение неоднородного уравнения:
Найдем частное решение, удовлетворяющее начальным условиям .
Технически поиск решения осуществляется стандартным способом, который рассматривался в статье Неоднородные дифференциальные уравнения второго порядка.
Держитесь, сейчас будем находить производную от найденного общего решения:
Вот такое вот безобразие. Упрощать его не обязательно, легче сразу составить систему уравнений. В соответствии с начальными условиями :
Подставим найденные значения констант 
в общее решение:
В ответе логарифмы можно немного запаковать.
Ответ: частное решение: 
Как видите, трудности могут возникнуть в интегралах и производных, но никак не в самом алгоритме метода вариации произвольных постоянных. Это не я вас запугал, это всё сборник Кузнецова!
Для расслабления заключительный, более простой пример для самостоятельного решения:
Пример 7
Решить задачу Коши
, 
Пример несложный, но творческий, когда составите систему, внимательно на неё посмотрите, прежде чем решать;-)
Конец.
Желаю успехов!
Решения и ответы:
Пример 3: Решение: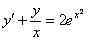 
Данное ДУ является линейным неоднородным. Используем метод вариации произвольных постоянных. Решим вспомогательное уравнение:
Разделяем переменные и интегрируем:
Общее решение: 
В неоднородном уравнении проведем замену:
Выполним подстановку:
Таким образом, общее решение:
Найдем частное решение, соответствующее заданному начальному условию:
Ответ: частное решение: 
Пример 5: Решение: Используем метод вариации произвольных постоянных.
Найдем общее решение соответствующего однородного уравнения:
– сопряженные комплексные корни, поэтому общее решение: 
.
Общее решение неоднородного уравнения ищем в виде: 
Составим систему:
В данном случае:
, 
, 
,
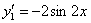Таким образом:
Систему решим по формулам Крамера:
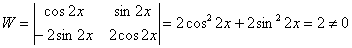, значит, система имеет единственное решение.
В результате:
Ответ: общее решение:
Пример 7: Решение: Используем метод вариации произвольных постоянных.
Найдем общее решение соответствующего однородного уравнения:
– кратные действительные корни, поэтому общее решение:
.
Общее решение неоднородного уравнения ищем в виде: 
Составим систему:
В данном случае:
, 
, 
Таким образом:
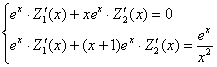
Кто-то будет мучиться с экспонентами, но счастье – вовремя заметить, что каждое уравнение можно сократить на 
!
Систему решим по формулам Крамера:
, значит, система имеет единственное решение.
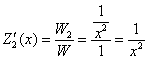
В результате общее решение:
Найдем частное решение, соответствующее начальным условиям .
Подставим найденные значения констант в общее решение:
Ответ: частное решение: 
Дата добавления: 2015-09-10; просмотров: 133 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Метод вариации произвольной постоянной для линейного неоднородного уравнения первого порядка | | | Find synonyms to the following words |