
Читайте также:
|
Лабораторная работа №1.
Исследование статической и динамической характеристики термопары.
Цель работы.
1.1. Ознакомиться с термоэлектрическим методом измерения температуры
1.2. Ознакомиться со схемами включения измерительногo прибора в цепь термопары.
1.3. Экспериментально получить статическую и динамическую характеристики термопары.
1.4. Определить математическую модель термопары.
Теоретическая часть.
В основу метода измерения температуры с помощью термопары положен термоэлектрический эффект: в замкнутой цепи, состоящей из двух разнородных проводников, возникает электрический ток, если места соединения (спаи) имеют разную температуру.
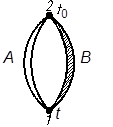 Рис. 1
Рис. 1
|  Рис. 2
Рис. 2
|
Цепь, состоящая из двух разнородных проводников, спаянных между собой называется термопарой, а проводники A и B, образующие термопару - термоэлектродами (рис. 1). Спай термопары, помещенный в зону измерения и имеющий температуру t, называется рабочим или горячим. Спай, имеющий температуру t 0, называется свободным или холодным. Если температуры спаев t и t0 не равны, то в замкнутой цепи будет протекать электрический ток. Направление этого тока зависит от соотношения температуры спаев, т.е. для нашего случая когда t > t 0ток пойдет от термоэлектрода А к термоэлектроду В. Термоэлектрод А называется термоположительным, термоэлектрод В - термоотрицательным.
При размыкании такой цепи на её концах может быть измерена так называемая термоэлектродвижущая сила (ТЭДС) (рис. 2).
Для замкнутой цепи, показанной на рис. 1, результирующая термо ЭДС составит:
EAB (t, t 0)= eAB (t)+ eBA (t 0) (1)
где eAB (t) и eBA (t 0) - контактные термо ЭДС в соответствующих спаях.
Если спаи 1 и 2 имеют одну и ту же температуру, например t 0, то контактные термо ЭДС в каждом спае равны между собой и действют навстречу, и поэтому результирующая термо ЭДС такого контура EAB (t 0, t 0) равна нулю, т.е.
EAB (t 0, t 0) = eAB (t 0) - eAB (t 0) = 0 (2)
или с учетом того, что
eAB (t 0) = - eBA (t 0) (3)
EAB (t 0, t 0) = eAB (t 0) + eBA (t 0) = 0 (4)
Подставив (3) в (1) получим
EAB (t, t 0) = eAB (t) + eBA (t 0) (5)
Уравнение (5) называется основным уравнением термопары, из него следует, что возникающая в контуре термо ЭДС EAB (t, t 0), зависят от разности функций температур t и t 0. Если сделать t 0 = const, то eAB (t 0) = c = const и
 (6)
(6)
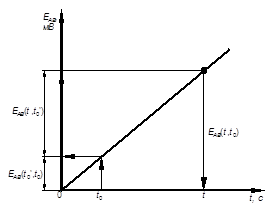 Рис. 3. графическое введение поправки на температуру свободных концов термопары
Рис. 3. графическое введение поправки на температуру свободных концов термопары
|
Зависимость (6) определяется экспериментально путем градуировки и последующего табулирования или построением графика зависимости термо ЭДС от температуры. В процессе градуировки температура свободных концов термопары должна поддерживаться постоянной, и значение её стандартизировано на уровне t 0=0 °C.
В рабочих условиях температура t 0,как правило, отличается от градировочной, что приводит к изменению значения ТЭДС.
Это обстоятельство вызывает необходимость введения поправки в показания прибора.
При этом используется соотношение:
EAB (t, t 0) = EAB (t, t 0') + EAB (t 0', t 0) (7)
где EAB (t, t 0) - значение ТЭДС термопары при температуре свободных концов t 0, равной градуировочной.
EAB (t, t 0') - значение ТЭДС термопары при действительной температуре свободных концов t 0' (показания прибора).
EAB (t 0', t) - поправка, которая должна быть внесена в показания прибора при t 0' t 0.
Если t 0' < t 0, то значения ТЭДС термопары завышены по сравнению с табличными данными и поправка берется со знаком плюс.
Если действительная температура свободных концов t0' известна, то величину поправки можно определить по градуировочной кривой, как показано на рис.3
Поправку можно определить и по градуировочной таблице 2 (см. приложение 2).
Несмотря на то, что любые два проводника создают в паре между собой ТЭДС, лишь ограниченное число термоэлектродов используется для создания термопар.
К материалам термоэлектродов предъявляется ряд требований:
- однозначная и по возможности близкая к линейной зависимость ТЭДС от температуры;
- жаростойкость и механическая прочность;
- химическая инертность
- термоэлектрическая однородность материала проводника по длине;
- технологичность изготовления;
- стабильность и воспроизводимость термоэлектрических свойств.
В настоящее время в основном применяют пять стандартных градуировок термопар (таблица 1)
| Таблица 1 | |||
| Термопара | Диапазон измеряемой температуры, ° С | Предельная температура при кратковременном применении, ° С | Допустимые отклонения, ° С |
| Хромель – копель (ТХК) | –50 - 600 | (2,2 - 5,8) | |
| Хромель – алюмель (ТХА) | –50 - 1000 | (4,0 - 9,7) | |
| Платинородий – платина (ТПП) | 0 - 1300 | (1,2 - 3,6) | |
| Платинородий – платинородий (ТПР) | 300 - 1600 | (3,2 - 5,2) | |
| Вольфрамрений – вольфрамрений (ТВР) | 0 - 2200 | (5,4 - 9,7) |
Для предохранения от механических повреждений и вредного влияния объекта измерения термоэлектроды термопары помещают в защитную арматуру.
В качестве средств измерений, работающих в комплекте с термопарой, используются милливольтметры, потенциометры и нормирующие преобразователи.
В данной работе исследующиеся статические и динамические характеристики термопары.
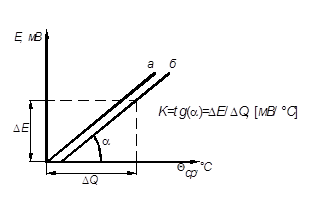 рис. 4. статические характеристики термопары: а - идеальная, б - реальная
рис. 4. статические характеристики термопары: а - идеальная, б - реальная
|
Статической характеристикой термопары называется зависимость ТЭДС EAB от температуры измеряемой среды Θ ср в равновесном состоянии.
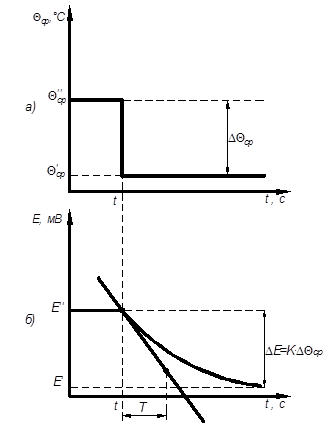 Рис. 5. динамические характеристики: а - скачок температуры; б – изменение ТЭДС – E, соответствующая данному скачку
Рис. 5. динамические характеристики: а - скачок температуры; б – изменение ТЭДС – E, соответствующая данному скачку
|
Зависимость, выраженная уравнением (6), представляет собой уравнение идеальной статической характеристики термопары, которая строится по градуировочной таблице (приложение, таблица 2).
Реальная статическая характеристика определяется в результате эксперимента.
Статические характеристики термопары приведены на рис. 4.
Динамическая (временная) характеристика термопары представляет собой зависимость изменения ТЭДС во времени при скачкообразном изменении температуры измеряемой среды (рис. 5)
Изменение ТЭДС - E, соответствующие данному скачку температуры Θ ср;
Математическая модель термопары описывается дифференциальным уравнением:
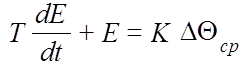 (8)
(8)
где E - ТЭДС термопары, мВ
Θ ср - скачок температуры, °С
Т - постоянная времени, °С
К - коэффициент усиления, мВ/°С
Решение уравнения (8)для случая убывающей экспоненты имеет вид:
E = K · Θ ср ·e(- t / T) (9)
где t - время, с.
Коэффициент усиления может быть определен как по статической характеристике (рис. 4), так и по динамической (рис. 5 а, б).
Постоянная времени, Т определяется, как проекция касательной к любой точке экспоненты на ось времени (до значения Е ' соответствующее ' ср). Из свойств экспоненты известно, что проекция касательной к любой точке экспоненты на ось времени есть величина постоянная. Под постоянной времени можно условно понимать время, в течение которого выходная величина после скачкообразного изменения входной величины, достигнет нового установившегося значения, изменяясь с постоянной скоростью.
Дата добавления: 2015-09-11; просмотров: 92 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Назовите причины жировой инфильтрации печени. | | | Приложение 1. |