Теории первого порядка. Модель теории. Выполнимая теория. Примеры теорий 1-го порядка: теория графов, теория групп.
Теория строгого частичного порядка без максимальных элементов – выполнимая теория, не имеющая конечных моделей.
Свободная подстановка терма вместо переменной в формулу.
1. Доказать несправедливость утверждений:
1) «Если функция непрерывна в точке, то она и дифференци-
руема в этой точке»;
2) «Если предел n -го члена числового ряда равен нулю, то ряд
сходится»;
3) «Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником»;
4) «Если функция интегрируема на отрезке, то она непрерывна на нем»;
5) «Если функция интегрируема на отрезке, то она монотонна на нем»;
6) «Если числовая последовательность имеет предел, то она монотонна»;
7) «Если числовая последовательность ограничена, то она имеет предел»;
8) «Если формула логики предикатов выполнима, то она общезначима»;
2. В следующих предложениях вместо многоточия поставьте слова «необходимо, но недостаточно» или «достаточно, но ненеобходимо» или же «не необходимо и недостаточно», а где возможно «необходимо и достаточно» так, чтобы получилось истинное утверждение:
1) Для того, чтобы четырехугольник был прямоугольным, …,чтобы длины его диагоналей были равны.
2) Для того, чтобы сумма четного числа натуральных чисел была четным числом, …, чтобы каждое слагаемое было четным.
4) Для того чтобы функция была интегрируема на отрезке, …, чтобы она была ограничена на нем.
5) Для того чтобы функция была интегрируема на отрезке, …, чтобы онабыла непрерывна на нем.
6) Для того чтобы окружность можно было вписать в четырехугольник, …, чтобы суммы длин его противоположных сторон были равны.
7) Для того чтобы множество A было счетным, …, чтобы его элементы можно было записать в виде нумерованной последовательности.
8) Для того чтобы числовая последовательность имела предел, …, чтобы она была ограниченной.
9) Для того чтобы числовая последовательности имела предел, …, чтобы она была монотонной и ограниченной.
Литература:[2,3,4,7,16,17,19,21,23,24,25]
Учебно-методическая литература:[2]
Тема 36. Классическое исчисление предикатов сигнатуры 
.
Классическое исчисление предикатов сигнатуры (
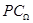). Вывод, теоремы, вывод из данного множества формул. Теорема дедукции для .
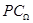Допустимые правила и теоремы исчисления предикатов: правило Бернайса; правила монотонности для кванторов; формулы
,
,
,
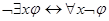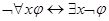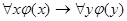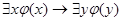
(с ограничениями).
Леммы о двойной подстановке в термы и формулы. Теорема корректности для .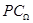
1. Среди следующих предложений выделите предикаты, для каждого из
предикатов укажите одну из возможных областей определения и в соот-
ветствии с ней множество истинности:
1) Луна есть спутник Венеры;
2) Планеты x и y принадлежат Солнечной системе;
3) Любое простое число p не имеет делителей, отличных от себя и 1.
2. Пусть 
и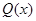 
- такие одноместные предикаты, заданные над одним и тем же множеством М, что высказывание:
3. Перечислите свободные и связанные вхождения каждой
из переменных в каждой из следующих формул:
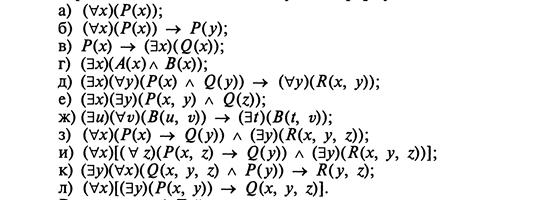
4. Докажите, что следующие формулы являются теоремами формализованного исчисления предикатов, для чего постройте выводы этих формул из аксиом:
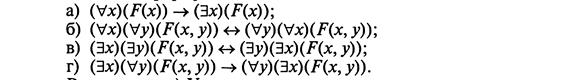
Литература:[2,3,4,7,16,17,19,21,23,24,25]
Учебно-методическая литература:[2]
Дата добавления: 2015-09-12; просмотров: 118 | Поможем написать вашу работу | Нарушение авторских прав |