
Читайте также:
|
Грабитель, проникший в банк, обнаружил в сейфе k золотых слитков, массами w 1, w 2,..., w k килограмм. При этом грабитель может унести не более W килограмм. Определите набор слитков, который должен взять грабитель, чтобы унести как можно больше золота.
Эта задача является частным случаем задачи об укладке рюкзака. Сформулируем ее в общем случае.
Дано k предметов, i -й предмет имеет массу w i > 0 и стоимость p i > 0. Необходимо выбрать из этих предметов такой набор, чтобы суммарная масса не превосходила заданной величины W (вместимость рюкзака), а суммарная стоимость была максимальна. Другими словами, нужно определить набор бинарных величин (b 1, b 2,..., b k), такой, что
b 1 w 1 + b 2 w 2 +...+ b k w k 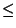 W,
W,
а величина b 1 p 1 + b 2 p 2 +...+ b k p k -- максимальная. Величина b i равна 1, если i -й предмет включается в набор, и равна 0 в противном случае.
Задача укладки рюкзака очень сложна. Если перебирать всевозможные подмножества данного набора из k предметов, то получится решение сложности не менее чем O (2k). В настоящее время неизвестен (и, скорее всего, вообще не существует) алгоритм решения этой задачи, сложность которого является многочленом от k.
Мы рассмотрим решение данной задачи для случая, когда все входные данные -- целочисленные, сложность которого будет O (kW).
Рассмотрим следующую функцию. Пусть A (s, n) есть максимальная стоимости предметов, которые можно уложить в рюкзак максимальной вместимости n, если можно использовать только первые s предметов из заданных k.
Зададим краевые значения функции A (s, n).
Если s = 0, то A (0, n) = 0 для всех n (ни один предмет нельзя брать, поэтому максимальная стоимость равна 0).
Если n = 0, то A (s, 0) = 0 для всех s (можно брать любые из первых s предметов, но вместимость рюкзака равна 0).
Теперь составим рекуррентное соотношение в общем случае. Необходимо из предметов с номерами 1,..., s составить рюкзак максимальной стоимости, чей вес не превышает n. При этом возможно два случая: когда в максимальный рюкзак включен предмет с номером s и когда предмет s не попал в максимальный рюкзак.
Если предмет s не попал в максимальный рюкзак массы n, то максимальный рюкзак будет составлен только из предметов с номерами 1,..., s - 1, следовательно, A (s, n) = A (s - 1, n).
Если же в максимальный рюкзак включен предмет s, то масса оставшихся предметов не превышает n - w s, а от добавления предмета s общая стоимость рюкзака увеличивается на p s. Значит, A (s, n) = A (s - 1, n - w s) + p s. Теперь из двух возможных вариантов составить рюкзак массы, не превосходящей n, из предметов 1,..., s нужно выбрать наилучший:
A (s, n) = max 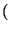 A (s - 1, n), A (s - 1, n - w s) + p s
A (s - 1, n), A (s - 1, n - w s) + p s  .
.
Теперь составим программу. Будем считать, что веса предметов хранятся в массиве w[1],..., w[k], а их стоимости в массиве p[1],..., p[k]. Значения функции A (s, n), где 0 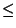 s
s 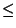 k, 0
k, 0 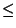 n
n 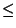 W, будем хранить в массиве A[k+1][W+1].
W, будем хранить в массиве A[k+1][W+1].
int A[k+1][W+1];
for(n=0;n<=W;++n) // Заполняем нулевую строчку
A[0][n]=0;
for(s=1;s<=k;++s) // s - максимальный номер предмета,
{ // который можно использовать
for(n=0;n<=W;++n) // n - вместимости рюкзака
{
A[s][n]=A[s-1][n];
if (n>=w[s] && (A[s-1][n-w[s]]+p[s] > A[s][n]))
A[s][n] = A[s-1][n-w[s]]+p[s];
}
}
В результате исполнения такого алгоритма в элементе массива A[k][W] будет записан ответ на поставленную задачу. Легко видеть, что сложность этого алгоритма, равно как и объем используемой им памяти, являются величиной O (kW).
Рассмотрим пример работы этого алгоритма. Пусть максимальная вместимость рюкзака W = 15, количество предметов k = 5, их стоимости и массы таковы:
w 1 = 6, p 1 = 5, w 2 = 4, p 2 = 3, w 3 = 3, p 3 = 1,
w 4 = 2, p 4 = 3, w 5 = 5, p 5 = 6.
В приведенной ниже таблице указаны значения заполненного массива A[k+1][W+1].
| s = 0 | |||||||||||||||||
| s = 1 | |||||||||||||||||
| s = 2 | |||||||||||||||||
| s = 3 | |||||||||||||||||
| s = 4 | |||||||||||||||||
| s = 5 |
Первая строка массива соответствует значениям A (0, n). Поскольку ни одного предмета брать нельзя, то строка заполнена нулями: из пустого множества предметов можно составить рюкзак нулевой массы.
Вторая строка массива соответствует значению s = 1, то есть рюкзак можно составлять только из первого предмета. Вес этого предмета w 1 = 6, а его стоимость p 1 = 5. Поэтому при n < 6 мы не можем включить этот предмет в рюкзак и значение A (1, n) равно 0 при n < 6. Если n 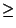 w 1, то мы можем включить первый предмет в рюкзак, а поскольку других предметов нет, то A (1, n) = 5 (так как p 1 = 5).
w 1, то мы можем включить первый предмет в рюкзак, а поскольку других предметов нет, то A (1, n) = 5 (так как p 1 = 5).
Рассмотрим третью строку массива, соответствующую двум предметам (s = 2). Добавляется второй предмет, более легкий и менее ценный, чем первый (w 2 = 4, p 2 = 3). Поэтому A (2, n) = 0 при n < 4 (ни один предмет взять нельзя), A (2, n) = 3 при n = 4 и n = 5 (в рюкзак включается предмет номер 2 ценности 3), A (2, n) = 5 при 6 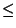 n
n 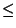 9 (при данном n выгоднее в рюкзак включить предмет 1, поскольку его ценность выше) и, наконец, A (2, n) = 8 при n
9 (при данном n выгоднее в рюкзак включить предмет 1, поскольку его ценность выше) и, наконец, A (2, n) = 8 при n 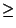 10 (при данной вместимости рюкзака можно взять оба предмета).
10 (при данной вместимости рюкзака можно взять оба предмета).
Аналогично заполняются остальные строки массива, при заполнении элемента A (s, n) рассматривается две возможности: включать или не включать предмет с номером s.
Как теперь вывести на экран тот набор предметов, который входит в максимальный рюкзак? Сравним значение A[k][W] со значением A[k-1][W]. Если они равны, то максимальный рюкзак можно составить без использования предмета с номером k. Если не равны, то предмет c номером k обязательно входит в максимальный рюкзак. В любом случае, задача печати рюкзака сводится к задаче печати рюкзака для меньшего числа предметов. Напишем это в виде рекурсивной функции Print(int s, int n), которая по параметрам s и n печатает номера предметов, входящих в максимальный рюкзак массой не более n и составленный из предметов 1,..., s:
void Print(int s, int n)
{
if (A[s][n]==0) // максимальный рюкзак для параметров (s,n)
return; // имеет нулевую ценность,
// поэтому ничего не выводим
else if (A[s-1][n] == A[s][n])
Print(s-1,n); // можно составить рюкзак без предмета s
else
{
Print(s-1,n-w[s]); // Предмет s должен обязательно
cout<<s<<endl; // войти в рюкзак
}
}
Для печати искомого рюкзака необходимо вызвать функцию с параметрами (k,W).
В приведенном примере для печати максимального рюкзака вызовем функцию Print(5,15). Поскольку A (5, 15) = 14, а A (4, 15) = 12 (с использованием только первых 4 предметов мы можем собрать рюкзак максимальной стоимости 12, а с использованием всех 5 предметов -- стоимости 14), предмет номер 5 обязательно входит в рюкзак. Далее рассмотрим A (4, 10) (общая вместимость рюкзака уменьшилась на вес включенного предмета). Поскольку A (4, 10) = A (3, 10) = A (2, 10) = 8, то мы можем исключить из рассмотрения предметы номер 4 и 3 -- можно собрать рюкзак вместимости 10 и стоимости 8 только из первых двух предметов. Для этого необходимо включить оба этих предмета. Таким образом, оптимальный рюкзак будет состоять из предметов 1, 2, 5, его масса будет равна 6 + 4 + 5 = 15, а стоимость -- 5 + 3 + 6 = 14.
Можно составить рюкзак и по-другому. Поскольку вес предмета 4 равен двум, его стоимость p 4 равна трём, а A (4, 10) = A (3, 8) + p 4, то мы можем включить в наш рюкзак предмет 4. Теперь рассмотрим A (3, 8) = 5 -- как составить рюкзак массы не более 8 и стоимости 5 из первых трех предметов. Поскольку A (3, 8) = A (2, 8) = A (1, 8) = 5, то мы исключаем из рассмотрения предметы 3 и 2, но включаем предмет 1. Получим рюкзак из предметов 1, 4, 5, его масса будет 6 + 2 + 5 = 13 и стоимость также равна 5 + 3 + 6 = 14. Поскольку стоимость обоих полученных рюкзаков получилась одинаковой, а масса в каждом случае не превосходит максимально допустимого значения W = 15, то оба решения подходят.
Дата добавления: 2014-11-24; просмотров: 170 | Поможем написать вашу работу | Нарушение авторских прав |
|