
|
Читайте также: |
Грабитель, проникший в банк, обнаружил в сейфе k золотых слитков, массами w 1, w 2,..., w k килограмм. При этом грабитель может унести не более W килограмм. Определите набор слитков, который должен взять грабитель, чтобы унести как можно больше золота.
Эта задача является частным случаем задачи об укладке рюкзака. Сформулируем ее в общем случае.
Дано k предметов, i -й предмет имеет массу w i > 0 и стоимость p i > 0. Необходимо выбрать из этих предметов такой набор, чтобы суммарная масса не превосходила заданной величины W (вместимость рюкзака), а суммарная стоимость была максимальна. Другими словами, нужно определить набор бинарных величин (b 1, b 2,..., b k), такой, что
b 1 w 1 + b 2 w 2 +...+ b k w k 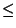 W,
W,
а величина b 1 p 1 + b 2 p 2 +...+ b k p k -- максимальная. Величина b i равна 1, если i -й предмет включается в набор, и равна 0 в противном случае.
Задача укладки рюкзака очень сложна. Если перебирать всевозможные подмножества данного набора из k предметов, то получится решение сложности не менее чем O (2k). В настоящее время неизвестен (и, скорее всего, вообще не существует) алгоритм решения этой задачи, сложность которого является многочленом от k.
Мы рассмотрим решение данной задачи для случая, когда все входные данные -- целочисленные, сложность которого будет O (kW).
Рассмотрим следующую функцию. Пусть A (s, n) есть максимальная стоимости предметов, которые можно уложить в рюкзак максимальной вместимости n, если можно использовать только первые s предметов из заданных k.
Зададим краевые значения функции A (s, n).
Если s = 0, то A (0, n) = 0 для всех n (ни один предмет нельзя брать, поэтому максимальная стоимость равна 0).
Если n = 0, то A (s, 0) = 0 для всех s (можно брать любые из первых s предметов, но вместимость рюкзака равна 0).
Теперь составим рекуррентное соотношение в общем случае. Необходимо из предметов с номерами 1,..., s составить рюкзак максимальной стоимости, чей вес не превышает n. При этом возможно два случая: когда в максимальный рюкзак включен предмет с номером s и когда предмет s не попал в максимальный рюкзак.
Если предмет s не попал в максимальный рюкзак массы n, то максимальный рюкзак будет составлен только из предметов с номерами 1,..., s - 1, следовательно, A (s, n) = A (s - 1, n).
Если же в максимальный рюкзак включен предмет s, то масса оставшихся предметов не превышает n - w s, а от добавления предмета s общая стоимость рюкзака увеличивается на p s. Значит, A (s, n) = A (s - 1, n - w s) + p s. Теперь из двух возможных вариантов составить рюкзак массы, не превосходящей n, из предметов 1,..., s нужно выбрать наилучший:
A (s, n) = max 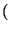 A (s - 1, n), A (s - 1, n - w s) + p s
A (s - 1, n), A (s - 1, n - w s) + p s  .
.
Теперь составим программу. Будем считать, что веса предметов хранятся в массиве w[1],..., w[k], а их стоимости в массиве p[1],..., p[k]. Значения функции A (s, n), где 0 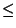 s
s 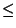 k, 0
k, 0 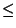 n
n 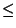 W, будем хранить в массиве A[k+1][W+1].
W, будем хранить в массиве A[k+1][W+1].
int A[k+1][W+1];
for(n=0;n<=W;++n) // Заполняем нулевую строчку
A[0][n]=0;
for(s=1;s<=k;++s) // s - максимальный номер предмета,
{ // который можно использовать
for(n=0;n<=W;++n) // n - вместимости рюкзака
{
A[s][n]=A[s-1][n];
if (n>=w[s] && (A[s-1][n-w[s]]+p[s] > A[s][n]))
A[s][n] = A[s-1][n-w[s]]+p[s];
}
}
В результате исполнения такого алгоритма в элементе массива A[k][W] будет записан ответ на поставленную задачу. Легко видеть, что сложность этого алгоритма, равно как и объем используемой им памяти, являются величиной O (kW).
Рассмотрим пример работы этого алгоритма. Пусть максимальная вместимость рюкзака W = 15, количество предметов k = 5, их стоимости и массы таковы:
w 1 = 6, p 1 = 5, w 2 = 4, p 2 = 3, w 3 = 3, p 3 = 1,
w 4 = 2, p 4 = 3, w 5 = 5, p 5 = 6.
В приведенной ниже таблице указаны значения заполненного массива A[k+1][W+1].
| s = 0 | |||||||||||||||||
| s = 1 | |||||||||||||||||
| s = 2 | |||||||||||||||||
| s = 3 | |||||||||||||||||
| s = 4 | |||||||||||||||||
| s = 5 |
Первая строка массива соответствует значениям A (0, n). Поскольку ни одного предмета брать нельзя, то строка заполнена нулями: из пустого множества предметов можно составить рюкзак нулевой массы.
Вторая строка массива соответствует значению s = 1, то есть рюкзак можно составлять только из первого предмета. Вес этого предмета w 1 = 6, а его стоимость p 1 = 5. Поэтому при n < 6 мы не можем включить этот предмет в рюкзак и значение A (1, n) равно 0 при n < 6. Если n 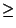 w 1, то мы можем включить первый предмет в рюкзак, а поскольку других предметов нет, то A (1, n) = 5 (так как p 1 = 5).
w 1, то мы можем включить первый предмет в рюкзак, а поскольку других предметов нет, то A (1, n) = 5 (так как p 1 = 5).
Рассмотрим третью строку массива, соответствующую двум предметам (s = 2). Добавляется второй предмет, более легкий и менее ценный, чем первый (w 2 = 4, p 2 = 3). Поэтому A (2, n) = 0 при n < 4 (ни один предмет взять нельзя), A (2, n) = 3 при n = 4 и n = 5 (в рюкзак включается предмет номер 2 ценности 3), A (2, n) = 5 при 6 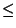 n
n 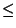 9 (при данном n выгоднее в рюкзак включить предмет 1, поскольку его ценность выше) и, наконец, A (2, n) = 8 при n
9 (при данном n выгоднее в рюкзак включить предмет 1, поскольку его ценность выше) и, наконец, A (2, n) = 8 при n 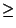 10 (при данной вместимости рюкзака можно взять оба предмета).
10 (при данной вместимости рюкзака можно взять оба предмета).
Аналогично заполняются остальные строки массива, при заполнении элемента A (s, n) рассматривается две возможности: включать или не включать предмет с номером s.
Как теперь вывести на экран тот набор предметов, который входит в максимальный рюкзак? Сравним значение A[k][W] со значением A[k-1][W]. Если они равны, то максимальный рюкзак можно составить без использования предмета с номером k. Если не равны, то предмет c номером k обязательно входит в максимальный рюкзак. В любом случае, задача печати рюкзака сводится к задаче печати рюкзака для меньшего числа предметов. Напишем это в виде рекурсивной функции Print(int s, int n), которая по параметрам s и n печатает номера предметов, входящих в максимальный рюкзак массой не более n и составленный из предметов 1,..., s:
void Print(int s, int n)
{
if (A[s][n]==0) // максимальный рюкзак для параметров (s,n)
return; // имеет нулевую ценность,
// поэтому ничего не выводим
else if (A[s-1][n] == A[s][n])
Print(s-1,n); // можно составить рюкзак без предмета s
else
{
Print(s-1,n-w[s]); // Предмет s должен обязательно
cout<<s<<endl; // войти в рюкзак
}
}
Для печати искомого рюкзака необходимо вызвать функцию с параметрами (k,W).
В приведенном примере для печати максимального рюкзака вызовем функцию Print(5,15). Поскольку A (5, 15) = 14, а A (4, 15) = 12 (с использованием только первых 4 предметов мы можем собрать рюкзак максимальной стоимости 12, а с использованием всех 5 предметов -- стоимости 14), предмет номер 5 обязательно входит в рюкзак. Далее рассмотрим A (4, 10) (общая вместимость рюкзака уменьшилась на вес включенного предмета). Поскольку A (4, 10) = A (3, 10) = A (2, 10) = 8, то мы можем исключить из рассмотрения предметы номер 4 и 3 -- можно собрать рюкзак вместимости 10 и стоимости 8 только из первых двух предметов. Для этого необходимо включить оба этих предмета. Таким образом, оптимальный рюкзак будет состоять из предметов 1, 2, 5, его масса будет равна 6 + 4 + 5 = 15, а стоимость -- 5 + 3 + 6 = 14.
Можно составить рюкзак и по-другому. Поскольку вес предмета 4 равен двум, его стоимость p 4 равна трём, а A (4, 10) = A (3, 8) + p 4, то мы можем включить в наш рюкзак предмет 4. Теперь рассмотрим A (3, 8) = 5 -- как составить рюкзак массы не более 8 и стоимости 5 из первых трех предметов. Поскольку A (3, 8) = A (2, 8) = A (1, 8) = 5, то мы исключаем из рассмотрения предметы 3 и 2, но включаем предмет 1. Получим рюкзак из предметов 1, 4, 5, его масса будет 6 + 2 + 5 = 13 и стоимость также равна 5 + 3 + 6 = 14. Поскольку стоимость обоих полученных рюкзаков получилась одинаковой, а масса в каждом случае не превосходит максимально допустимого значения W = 15, то оба решения подходят.
Адам», «индивид», «тұлға», «даралық» ұғымдарына сипаттама.
Адамды көптеген ғылымдар қарастырады: философия, әлеуметтану, этика, эстетика, педагогика, психология және т.т. әрбір ғылымның өзінің адамды зерттеу пәндері бар. Адамға әлеуметтік-психологиялық талдау жасау үшін: «адам», «индивид», «тұлға», «даралық» ұғымдарына қатысты нақты түсінік шегін белгілеуіміз керек.
Адам -жоғарғы психикалық қызметті арқасында меңгеру, жасау, өзгерту қабілетіне ие саналы биоәлеуметтік тіршілік иесі, қоғамдық-тарихи дамудың жемісі әрі сол қо,амдық өмір жемісі болып табылатын сананы таратушы. Өзіндік сана-сезімі адам сана дамуының филогенездік, онтогенездік дамуының шыңы. Адамда: биологиялық, психологиялық, педагогикалық, әлеуметтік сияқты құрылымдары бар. Ол құрылымдармен адам болмысы өлшенеді және олар бір-бірімен өзара байланысты. Олар: адамның жеке басына тән қайталанбас ерекшеліктерінің болатыны; адам бойындағы кісілік (тұлғлық) қасиеттердің болатыны. Ол аға ұрпақ жасаған мәдениетті меңгеруде қалыптасады. Егер адам жас кезінде қоғамнан тыс қалса, онда оның санасы, тілі, ойлауы, және вертикалда аяқ алысып болмайды. Адам әр түрлі еңбек және түрлі формадағы қоғамдық іс-әрекетке қатысу арқылы адамзатта қалыптасқан қасиеттерді ол өзінде өзіне тән адамдық қабілетерді дамытады.. Адам түсінігі көп жоспарлы. Адам қоғамда өмір сүреді. Ал адам бос өмір сүруі ешбір мүмкін емес. Оның тәні де жаны да айналасындағылармен қарым қатынас жасау үстінде тек әлеументтік әсер жағдайында ғана кісілік мәнге ие болады. Адамның санасының дамып, өсуі тікелей өзінің өмір сүріп отырған ортасына байланысты. Сондықтан адам психологиясын дұрыс ұғыну үшін: әлеументтік жағдайын білу керек; оның қандай ортаның өкілі екенін айыру; оның көзқарасы мен наным- сенімін бағыт- бағдарын білімі мен тәжірибесіне икем биімділігін анықтау керек. Міне, тек осы айтылғандардан кейін ғана, нақты мәліметтерден соң сол адам туралы пікір білдіруге мүмкіндік туады. Психология адамның даралық сипаттарын қарастырып, оның кісілік қасиеттерін өрістетуді мақсат тұтады.
Индивид (жеке адам) -тұқымқуалаушылық қасиеттердің жалпы генотипін тасымалдаушы, биоәлеуметтік тіршілік иесі. Адам дүниеге келгенде индивид болып туылады. Ол қоғамдық қатынастардың объектісі, әрі субъектісі. Қатынастар ықпалын сезіну мен бірге қатысушы, әрі оны терең бойлаушы. З.Фрейд ілімі бойынша, үнемі қоғам ішінде болып оның ықпалын сезінуші, әрі оған қарсы тұрушы биологиялық тұйық жан.
Тұлға -адамның қоғамдық санасы мен мінез-құлықты, адамзаттың қоғамдық-тарихи тәжірибесін меңгеруде қалыптасқан адамның әлеуметтік-психологиялық мәні. Тұлға қоғамдық қатынасты обьектісі мен жемісі ғана емес, сонымен бірге іс-әрекет, қатынас, сана, өзіндік сананың белсенді субьектісі. Тұлға болып туылмайды, ол әлеуметтік, мәдени даму нәтижесінде туындайды. Тұлға мақсатқа талпынушы ғана емес, сонымен бірге өзін-өзі ұйымдастыратын жүйе. Оның зейіні мен іс-әрекетінің обьектісі: сыртқы орта мен өзінің «Мендік» сезім болады. Осыған байланысты өзін -өзі реттеу, өзін-өзі ұстай білу, қабілеті мен қасиет көрсетеді. Тұлға болу дегеніміз -белсенді түрде өмірлік позицясы бар және ішкі қажеттілікке байланысты таңдау жасай білу, келген шешімінің зардабын бағалау және өзі қоғамның алдында жауап беру, үнемі өзін-өзі және өзгелерді құруға түрлі әдіс, тәсілдерді меңгеріп өз мінез құлқын реттеуші.
Тұлғалық қасиеттер үш дәрежеде болады:
1. Әрбір адам ең алдымен адамзат қауымының мүшесі ретінде шыққан нәсілінен, ұлтынан, туысынан, туған жерінен тәуелсіз есті адамның барлық өкілдеріне ортақ жалпы қасиеттерді иелену. Олардың қатарына: қуану, қайыру, болжамдық, елді сүю, арамдық –зұлымдарға, әділетсіздіктерге, әділеттікке және т.б. көптеген рухани-психологиялық қасиеттер жатды.
2. Әр адамның физикалық ерекшеліктерінен жоғары жүйке жүйесінің қызметінен туындайтын және тек өз басына тән психологиялық өзгешеліктер. Бұлар, оның мінез-құлықында, сезім көрінісінде, темперментінде, қимыл мен жүріс тұрысында, сөйлеу ерекшелігінде, сыртқы әсерлерге қайтаратын жауаптарында, басқа адамдармен қарым-қатынсында т.б. тіршілік әрекеттерінде байқалады. Осы қайталанбайтын ерекшеліктерінің арқасында әр адамның басқаларға ұқсамайтын өзіндік қырлары туады. Бұл қырларының негізгі физиологиялық ерекшеліктерінде жатқанмен оған әрине өмір сүру ортасының да қатысы бар.
3. Адам белгілі бір елде, рухани дәстүрде белгілі дәрежеде жеткен материалдық және рухани мәдениет жемістерін сусындап өседі. Сол дәуірдің тарихи ортаның жемісі осының бәрі адамның жан-дүниесінде өзінің ізін қалдырады.
Тұлғаны анықтайтындар қатарыны: нені және қалай білетіндігі, нені және оны қалай бағатыны, нені және оны қалай жандандырады, кіммен және қалай қатынас жасайтыны, оның көркемдік қажеттілігі жән оны қалай қанағаттандыратындығына байланысты.
Ең негізгісі өзінің әрекетіне, шешіміне, тағдырына деген жауапкершілігіне сай өлшемі тұлғаны толық көрсетеді.
Даралық - түрлі тәжірибе, білім, пікір, сенім, мінез-құлық, темпераменттермен көрініс береді. Даралық негізгі параметрлері: себеп, темперамент, қабілет, мінез.
Эмоциялық, белсенділік темпераменттің екінші функциясы. Белсенділік пен өзін-өзі реттеу қабілетінің сипаттамасы. Даралықта-тұлға мен организм бірлікте қарастырылады.
Дата добавления: 2014-11-24; просмотров: 366 | Поможем написать вашу работу | Нарушение авторских прав |