Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Соединенные Штаты Америки

Одной из типичных задач линейного программирования является, так называемая, транспортная задача. Она возникает при планировании рациональных перевозок грузов. В одних случаях это означает определение такого плана перевозок, при котором их стоимость была бы минимальна, а в других - более важным является выигрыш во времени. Первая задача называется транспортной задачей по критерию стоимости, а вторaя - транспортной задачей по критерию времени.

Первая задача является частным случаем задачи линейного программирования и может быть решена симплексным методом. В силу особенностей этой задачи она решается проще.

Пусть в m пунктах отправления (А₁, А₂, …, А_m) находятся, соответственно, a_i (i=1, m) единиц однородного груза (запасы), который должен быть доставлен n потребителям (В₁, В₂, …, В_n) в количествах b_j (j=1, n) единиц (заявки). Заданы стоимости c_ij перевозок единицы груза из i-го пункта отправления j-му пункту потребления. Обозначим через x_ij ≥ 0 (i =1, m; j =1, n) количество единиц груза, перевозимого из i-го склада j-му потребителю; тогда переменные x_ij должны удовлетворять следующим ограничительным условиям:

1) 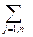x_ij = a_i (i = 1, m), (все запасы израсходованы);

2) x_ij = b_j (j = 1, n), (все заявки удовлетворены) (3.34)

3) x_ij ≥ 0.

Суммарные затраты на перевозки равны Ф = 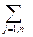(с_ij·x_ij).

Следовательно, требуется на множестве неотрицательных решений найти переменные x_ij, (i = 1, m; j = 1, n), удовлетворяющих указанным условиям и минимизирующих целевую функцию Ф.

Математическая модель транспортной задачи обладает следующими особенностями:

а) система ограничений задана в виде уравнений (задача задана в канонической форме);

б) коэффициенты при переменных в системе ограничений равны единице или нулю;

в) каждая переменная входит в систему ограничений два раза: один раз в сумму по i и один раз в сумму по j;

Транспортные задачи, в которых выполняется условие a_i = b_j, то есть, суммарные запасы равны суммарным потребностям, называются закрытыми транспортными задачами (закрытая модель транспортной задачи). В противном случае задача называется открытой (открытая модель транспортной задачи).

А. Закрытая транспортная задача является частным случаем задачи линейного программирования и методы ее решения представляют собой компактные интерпретации общих методов линейного программирования. Наиболее эффективные методы решения транспортной задачи основаны на методе последовательного улучшения плана (симплексный метод) и на методе последовательного сокращения невязок (венгерский метод).

Специфичная форма системы ограничений данной задачи позволяет существенно упростить обычный симплексный метод. Модификациями симплексного метода применительно к закрытой транспортной задаче являются распределительный метод и его разновидности ( метод северо-западного угла, метод минимальной стоимости, метод двойного предпочтения), а также метод потенциалов.

В. Открытая модель транспортной задачи имеет две разновидности:

а) суммарные запасы превышают суммарные потребности a_i > b_j;

б) суммарные потребности превышают суммарные запасы a_i < b_j;

Целевая функция одинакова в обоих случаях, изменяется только система ограничений.

Открытая задача решается приведением к закрытой модели.

В случае (а), когда суммарные запасы превышают суммарные потребности, вводится фиктивный (n+1)-ый потребитель, потребности которого равны

b_n+1 = a_i - b_j.

В случае (б), когда суммарные потребности превышают суммарные запасы, вводится фиктивный (m+1)-ый поставщик, запасы которого равны

a_m+1 = b_j - a_i

Стоимость перевозки единицы груза как до фиктивного потребителя, так и стоимость перевозки единицы груза от фиктивного поставщика полагают равными нулю, так как груз в обоих случаях не перевозится. После преобразований задача принимает вид закрытой модели и решается обычным способом.

2.Транспортная задача по критерию времени заключается в минимизации времени перевозок. Выразим время Т через времена t_ij и объемы x_ij (от i–го поставщика до j–го поставщика). Так как все перевозки заканчиваются в тот момент, когда кончается самая длительная из всех перевозок, то время Т есть максимальное из всех времен t_ij ненулевых перевозок, то есть, T = max t_ij,

^Xij>0

где символ х_ij>0 означает, что берется максимальное не из всех t_ij, а только из тех, для которых перевозки отличны от нуля.

Требуется, чтобы

Поставленная задача не является задачей линейного программирования, так как величина Т – нелинейная функция переменных х_ij. Эту задачу можно свести к решению задач линейного программирования, но не одной, а нескольких. А для непосредственного решения транспортной задачи по критерию времени применяется, так называемый «метод запрещенных клеток».

Соединенные Штаты Америки