
Читайте также:
|
Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция.
Степенной ряд- самый частый пример функционального ряда.
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: (a;b)
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости ряда представляет собой полуинтервал: [a;b) или (a:b].
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок:[a;b]
19.Степенные ряды. Интервал сходимости. Степенным рядом называется ряд типа а(0)+а(1)*х(квадрат)+а(2)*х(куб)+…+, где а-постоянные числа, называемые к-тами ряда. Множество значений х, при которых ряд сходится, называется областью сходимости.Область сходимости-некоторый интервал. Интервал сходимости является такой интервал от –r до +r, что для всякой точки x, лежащей в этом интервале, ряд сходится и притом абсолютно, а для точек х вне его-ряд расходится.
20.Ряд Маклорена. Ряд Тейлора.
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:f(x)=CИГМАf(n)(а)*(х-а)n /n!
Если a = 0, то такое разложение называется рядом Маклорена: f(x)=CИГМАf(n)(0)*xn/n!
21.Разложение функции в степенные ряды. Если функция  в некотором интервале раскладывается в степенной ряд по степеням
в некотором интервале раскладывается в степенной ряд по степеням  , то это разложение единственно и задается формулой:
, то это разложение единственно и задается формулой:

Примечания: Надстрочный индекс  в последнем слагаемом обозначает производную «энного» порядка.
в последнем слагаемом обозначает производную «энного» порядка.
Данная формула получила имя некоего англичанина Тейлора
22.Использование степенных рядов для приближенного вычисления. Пример-Пользуясь разложением в ряд sinx, вычислить sin20o с точностью до 0,0001.
Решение. Чтобы можно было пользоваться формулой (2), необходимо выразить значение аргумента в радианной мере. Получаем  . Подставляя это значение в формулу, получаем
. Подставляя это значение в формулу, получаем

Полученный ряд является знакочередующимся и удовлетворяет условиям Лейбница. Так как  , то этот и все последующие члены ряда можно отбросить, ограничиваясь первыми двумя членами. Таким образом,
, то этот и все последующие члены ряда можно отбросить, ограничиваясь первыми двумя членами. Таким образом,

23.Ряды Фурье.
Тригонометрическим рядом Фурье функции  называют функциональный ряд вида
называют функциональный ряд вида

| (1) |
где



Числа  ,
,  и
и 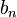 (
( ) называются коэффициентами Фурье функции
) называются коэффициентами Фурье функции  .
.
Дата добавления: 2015-01-30; просмотров: 192 | Поможем написать вашу работу | Нарушение авторских прав |