Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Дифф.уравнения с разделяющимися переменными.

Грубо говоря, в левой части нам нужно оставить только «игреки», а в правой части организовать только «иксы». Разделение переменных выполняется с помощью «школьных» манипуляций: вынесение за скобки, перенос слагаемых из части в часть со сменой знака, перенос множителей из части в часть по правилу пропорции и т.п.

Однородные дифф.уравнения.

Обыкновенное уравнение первого порядка 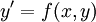называется однородным относительно x и y, если функция является однородной степени.

Дифф. уравнения, приводимые к однородным.

Линейные уравнения первого порядка. Метод Бернулли.

Линейным дифференциальным уравнением первого порядка называется уравнение вида

y ‘ + f(x)*y=ф(x). Удобным способом решения линейных уравнений является метод Бернулли. Пусть дано уравнение (1). Решение этого уравнения будем искать в виде произведения двух функций: y=u*v,где u=u(x) и v=v(x). Далее подставляем это значение вместо y и все решение сведется к решению системы уравнений с разделяющимися переменными.