Читайте также:
|
Понятие дифф. Уравнения, его решения.Дифф уравнения, как мат.модели физ.процессов.
Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).В зависимости от комбинаций произодных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных.
Дифф уравнения первого порядка. Их геометрическая интерпретация.Построение дифф.уравнения заданного семейства кривых.
Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную 
;
2) зависимую переменную 
(функцию);
3) первую производную функции: 
.
В некоторых случаях в уравнении первого порядка может отсутствовать «икс» или (и) «игрек» – важно чтобы в ДУ была первая производная , и не было производных высших порядков – 
, 
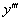и т.д.
Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество функций 
, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
Геометрический смысл- образования одной и той же прямой, называемой изоклином.
Дата добавления: 2015-01-30; просмотров: 119 | Поможем написать вашу работу | Нарушение авторских прав |