Читайте также:
|
Основание системы счисления – количество знаков или символов, используемых в данной системе счисления для изображения числа.
Позиционные системы счисления имеют ряд преимуществ перед непозиционными: удобство выполнения арифметических и логических операций, а также представление больших чисел, поэтому в цифровой технике применяются позиционные системы счисления.
Разряд – номер позиции в числе. Нумеруются справа налево, начиная с нуля.
Вес разряда – число, равное основанию системы счисления в степени номера разряда. В вычислительной технике используются позиционные системы счисления – двоичная (BIN) в качестве основной, десятичная (DEC) и шестнадцатеричная (HEX) в качестве вспомогательных, ранее использовалась восьмеричная (OCT).
Запись чисел может быть представлена в виде: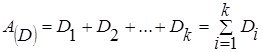 
,
где 
– запись числа A в СС D;
– символ системы, образующие базу.
По этому принципу построены непозиционные СС.
В общем же случае системы счисления:
.
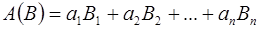Если положить, что 
, а 
, то получим позиционную СС. При 
мы имеем дело с десятичной СС.
На практике также используют другие СС:
| q | Название | Цифры |
| двоичная | 0,1 | |
| троичная | 0,1,2 | |
| восьмеричная | 0,...,7 | |
| шестнадцатиричная | 0,...,9,A,...,F |
Каждая СС имеет свои правила арифметики (таблица умножения, сложения). Поэтому, производя какие-либо операции над числами, надо помнить о СС, в которой они представлены.
Если основание системы q превышает 10, то цифры, начиная с 10, при записи обозначают прописными буквами латинского: A,B,...,Z. При этом цифре 10 соответствует знак 'A', цифре 11 – знак 'B' и т.д. В таблице ниже приводятся десятичные числа от 0 до 15 и их эквивалент в различных СС:
| q=10 | q=2 | q=16 |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
В позиционной СС число можно представить через его цифры с помощью следующего многочлена относительно q:
(1)
Выражение (1) формулирует правило для вычисления числа по его цифрам в q-ичной СС. Для уменьшения количества вычислений пользуются т.н. схемой Горнера. Она получается поочередным выносом q за скобки:
,
результат вычисления многочлена будет всегда получен в той системе счисления, в которой будут представлены цифры и основание и по правилам которой будут выполнены операции.
Дата добавления: 2015-01-30; просмотров: 76 | Поможем написать вашу работу | Нарушение авторских прав |