Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Эффект Комптона. Корпускулярно-волновой дуализм. Волны де Бройля.

Эффект Комптона (Комптон-эффект) — явление изменения длины волны электромагнитного излучения вследствие упругого рассеивания его электронами. При рассеянии фотона на покоящемся электроне частоты фотона и (до и после рассеяния соответственно) связаны соотношением:

где — угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн:

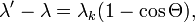
где 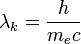— комптоновская длина волны электрона.

Для электрона м. Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом. В классической электродинамике рассеяние электромагнитной волны на заряде (томсоновское рассеяние) не сопровождается уменьшением её частоты.

Объяснить эффект Комптона в рамках классической электродинамики невозможно. С точки зрения классической физики электромагнитная волна является непрерывным объектом и в результате рассеяния на свободных электронах изменять свою длину волны не должна. Эффект Комптона является прямым доказательством квантования электромагнитной волны, другими словами подтверждает существование фотонов. Эффект Комптона является ещё одним доказательством справедливости корпускулярно-волнового дуализма микрочастиц.

Корпускуля́рно-волново́й дуали́зм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Во́лны де Бро́йля — волны, связанные с любыми микрочастицами и отражающие их волновую природу.

Для частиц не очень высокой энергии, движущихся со скоростью (скорости света), импульс равен (где — масса частицы), и . Следовательно, длина волны де Бройля тем меньше, чем больше масса частицы и её скорость. Например, частице с массой в 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с м, что лежит за пределами доступной наблюдению области. Поэтому волновые свойства несущественны в механике макроскопических тел. Для электронов же с энергиями от 1 эВ до 10 000 эВ длина волны де Бройля лежит в пределах от ~ 1 нм до 10⁻² нм, то есть в интервале длин волн рентгеновского излучения. Поэтому волновые свойства электронов должны проявляться, например, при их рассеянии на тех же кристаллах, на которых наблюдается дифракция рентгеновских лучей. Де Бройль выдвинул идею о том, что волновой характер распространения, установленный для фотонов, имеет универсальный характер. Он должен проявляться для любых частиц, обладающих импульсом . Все частицы, имеющие конечный импульс , обладают волновыми свойствами, в частности, подвержены интерференции и дифракции.

Формула де Бройля устанавливает зависимость длины волны , связанной с движущейся частицей вещества, от импульса частицы:

где — масса частицы, — ее скорость, — постоянная Планка. Волны, о которых идет речь, называются волнами де Бройля.

Другой вид формулы де Бройля:

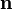где — волновой вектор, модуль которого — волновое число — есть число длин волн, укладывающихся на единицах длины, — единичный вектор в направлении распространения волны, Дж·с.

Длина волны де Бройля для нерелятивистской частицы с массой , имеющей кинетическую энергию

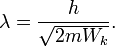
В частности, для электрона, ускоряющегося в электрическом поле с разностью потенциалов вольт

Формула де Бройля экспериментально подтверждается опытами по рассеянию электронов и других частиц на кристаллах и по прохождению частиц сквозь вещества. Признаком волнового процесса во всех таких опытах является дифракционная картина распределения электронов (или других частиц) в приемниках частиц.

Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным. Впрочем, наблюдать квантовые эффекты можно и в макроскопическом масштабе, особенно ярким примером этому служат сверхпроводимость и сверхтекучесть.

Фазовая скорость волн де Бройля свободной частицы

где — циклическая частота, — кинетическая энергия свободной частицы, — полная (релятивистская) энергия частицы, — импульс частицы, , — её масса и скорость соответственно, — длина дебройлевской волны. Последние соотношения — нерелятивистское приближение. Зависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию. Фазовая скорость волны де Бройля хотя и больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом).

Групповая скорость волны де Бройля равна скорости частицы :

.

Связь между энергией частицы и частотой волны де Бройля

Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат модуля амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определенные места в приёмниках — туда, где интенсивность волны де Бройля оказывается наибольшей. Частицы не обнаруживаются в тех местах, где, согласно статистической интерпретации, квадрат модуля амплитуды «волны вероятности» обращается в нуль.