Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Уравнение Шредингера. Частица в потенциальной яме.

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда не является функцией времени, можно записать в виде:

где функция 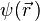должна удовлетворять уравнению:

которое получается из уравнения Шрёдингера (1) при подстановке в него указанной выше формулы для (2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называется стационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).

Выражение (2) является лишь частным решением зависящего от времени уравнения Шрёдингера (1), общее решение представляет собой линейную комбинацию всех частных решений вида (2). Зависимость функции от времени проста, но зависимость её от координаты не всегда имеет элементарный вид, так как уравнение (3) при одном выборе вида потенциальной функции совершенно отличается от того же уравнения при другом выборе этой функции. В действительности, уравнение (3) может быть решено аналитически лишь для небольшого числа частных типов функции .

Важное значение имеет интерпретация величины в уравнении (2). Она производится следующим путём: временна́я зависимость функции в уравнении (2) имеет экспоненциальный характер, причём коэффициент при в показателе экспоненты выбран так, что правая часть уравнения (3) содержит просто постоянный множитель . В левой же части уравнения (3) функция умножается на потенциальную энергию . Следовательно, из соображений размерности вытекает, что величина должна иметь размерность энергии. Единственной величиной с размерностью энергии, которая постоянна в механике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, что представляет собой полную энергию. Согласно физической интерпретации уравнения Шрёдингера, действительно является полной энергией частицы при движении, описываемом функцией .

Потенциа́льная я́ма – область пространства, где присутствует локальный минимум потенциальной энергии частицы.

Если в потенциальную яму попала частица, энергия которой ниже, чем необходимая для преодоления краёв ямы, то возникнут колебания частицы в яме. Амплитуда колебаний будет обусловлена собственной энергией частицы. Частица, находящаяся на дне потенциальной ямы, пребывает в состоянии устойчивого равновесия, то есть при отклонении частицы от точки минимума потенциальной энергии возникает сила, направленная в противоположную отклонению сторону. Если частица подчиняется квантовым законам, то даже несмотря на недостаток энергии она с определённой вероятностью может покинуть потенциальную яму (явление туннельного эффекта).

Потенциальный барьер — противоположное понятие. Это область пространства, где присутствует локальный максимум потенциальной энергии.

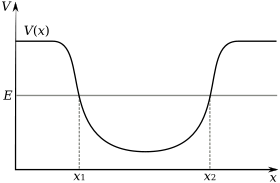
Потенциальная яма — участок от X₁ до X₂