Студопедия
Главная страница | Контакты | Случайная страница

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Среднее квадратическое отклонение

Читайте также:
  1. ВАЛЬГУСНОЕ ОТКЛОНЕНИЕ 1-ГО ПАЛЬЦА СТОПЫ
  2. Вопрос№ 31. Среднее число столкновений и средняя длина свободного пробега молекул
  3. Если все индивидуальные значения признака увеличить на 100 единиц, то среднее значение нового признака
  4. Какие причины не побуждают проблемную ситуацию «Отклонение времени движения автомобиля на маршруте от нормативного».
  5. Качественные показатели статистики грузовых и пассажирских перевозок (среднее расстояние перевозки, средняя густота перевозок)
  6. Начальное и среднее образование
  7. Оплата при отклонение от нормальных условий труда.
  8. Особенности воды как растворителя. Отклонение от законов Рауля и Вант-Гоффа для электролитов.
  9. Под средней длиной свободного пробега понимают среднее расстояние, которое проходит молекула между двумя последовательными соударениями.
  10. Современная модель общеобразовательной школы включает: начальное образование, базовое образование, полное среднее образование.

Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

Дисперсия 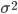- представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия простая:

Дисперсия взвешенная:

 

 

16.Билет

Дисперсия. Виды дисперсий и правила их сложения

 

Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:

1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:

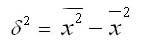
2. Взвешенная дисперсия (для вариационного ряда):

где n - частота (повторяемость фактора Х)



Дата добавления: 2015-01-30; просмотров: 144 | Поможем написать вашу работу | Нарушение авторских прав


lektsii.net - Лекции.Нет - 2014-2025 год. (0.006 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав