Читайте также:
|
Дисперсия портфеля из двух бумаг равна
,
риск равен
,
где 
– коэффициент корреляции[1] двух бумаг;
– риск i-ой бумаги;
– ценовая доля i-ой бумаги.
Доходность портфеля равна
,
где 
– эффективность i-ой бумаги.
Условие нормировки
.
Ковариация доходностей определяется как
;
.
Отсюда
; 
.
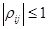При положительной корреляции дисперсия суммарного дохода увеличивается, при отрицательной она сокращается. В самом деле, при заметной отрицательной корреляции положительные отклонения от среднего дохода одних бумаг погашаются отрицательными отклонениями у других. И наоборот, при положительной корреляции отклонения суммируются, что увеличивает общую дисперсию и риск.
В случае полной корреляции
.
Для квадрата риска (дисперсии) портфеля имеем:
.
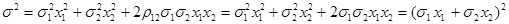Тогда риск равен
.
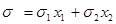Если инвестор формирует портфель минимального риска, то он должен включить в него бумагу одного типа, имеющую меньший риск. Если меньший риск имеет бумага первого типа, то получим портфель Х=(1,0) с доходностью 
.
При формировании портфеля максимальной доходности, в него необходимо включить только бумагу, имеющую большую доходность, в нашем случае бумагу 2. Получим портфель Х=(0.1) с доходностью 
.
В случае полной антикорреляции
.
Для квадрата риска (дисперсии) портфеля имеем:
.
Тогда риск равен
.
При полной антикорреляции возможен портфель нулевого риска.
Пример. Дан портфель из двух бумаг с доходностью и риском соответственно (0,2;0.5) и (0.4;0.7). Найти портфель нулевого риска и его доходность для случая полной антикорреляции.
Дата добавления: 2015-02-16; просмотров: 121 | Поможем написать вашу работу | Нарушение авторских прав |