Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Методы оценки акций

Оценка акций с постоянными дивидендами:

, (3.12)

где

Р_А(пос) – цена акции, ден. ед.;

D_Г – годовой дивиденд, ден. ед.;

R_A – ставка доходности акций, %.

Пример. АО выплачивает годовой дивиденд на акцию 0,35 руб. Необходимая ставка доходности по акциям составляет 15 %. Определите цену акции.

Решение:

Р_А(пос)= 0,35/0,15 = 2,33 руб.

Оценка акций с постоянным приростом дивидендов (Модель Гордона):

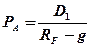, (3.13)

где

D₁ – ожидаемые дивиденды на акцию через год D₁ = D_o(1 + g);

R_A – необходимая доходность по акциям, %

g – темп прироста дивидендов.

Пример. Последний раз АО выплатило по каждой акции дивиденд в размере 0,25 руб. АО прогнозирует, что ее дивиденды будут ежегодно увеличиваться на 10 %. Определите цену акции, если необходимая ставка доходности по акциям составляет 15 %.

Решение:

Р₀=0,25х(1+0,1)/(0,15-0,10) = 5,5 руб.

Оценка акций с непостоянным приростом дивидендов:

, (3.14)

где

Р_А – рыночная цена акции, ден. ед.

D_n – ожидаемый годовой дивиденд на акцию.

R_A – текущая доходность акции, %;

n – срок использования акции, лет.

Пример. Инвестор купил акцию с прогнозом дивидендов в 1-й год 0,5 руб. и в последующие годы приростом на 0,05 руб. Норма текущей доходности 15 % в год. Акция куплена на 5 лет. Определить рыночную цену акции.

Решение:

Р ₀ = 0,5 / (1+0,15)¹ + 0,55 / (1+0,15)² + 0,60 / (1+0,15)³ + 0,65 / (1+0,15)⁴ + 0,70 / (1+0,15)⁵ = 1,96 руб.

Для анализа эффективности вложений инвестора в покупку акций Маойрова [] предлагает рассчитывать такие виды доходности: ставка дивиденда; текущая доходность акции для инвестора; текущая рыночная доходность; конечная и совокупная доходность.

Ставка дивиденда (d_c) определяется по такой формуле:

, (3.15)

где

d_C - ставка дивиденда, %;

D – величина выплачиваемых годовых дивидендов, руб.;

N – номинальная цена акции, руб.

Текущая доходность акции для инвестора – рендит (d_T), определяется по такой формуле:

, (3.16)

где

d_r – текущая доходность акции, %;

D – величина выплачиваемых годовых дивидендов, руб.;

P – цена приобретения акции, руб.

Текущая рыночная доходность (d_p) определяется соотношением величины дивидендов, которые уплачиваются к текущей рыночной цене акции:

, (3.17)

где

d_p – текущая рыночная доходность

D – величина выплачиваемых годовых дивидендов, руб.;

P₀ – текущая рыночная цена акции, руб.

Конечная доходность акции (d_k) может быть определена таким образом:

,

где

d_k – конечная доходность акции, %;

– средняя величина выплачиваемых годовых дивидендов, руб.;

Р – величина дивидендов, выплаченная за год, руб.

ΔР – прирост или снижение капитала инвестора, которая равняется разнице между ценой продажи акции и ценой приобретения акции, руб.;

n – количество лет, на протяжении которых инвестор владел акциями.

Совокупная доходность акций (d_c) является обобщающим показателем эффективности вложений инвестора в покупку акций. Она рассчитывается по такой формуле:

,

где

d_c - совокупная доходность акций, %;

D_i – величина дивидендов, выплачиваемых в i-м году, руб.

Конечная и совокупная доходность могут использоваться в том случае, когда инвестор продал акцию или планирует ее продать по цене, известной только ему.

Доход от прироста курсовой стоимости акций (d) определяется в том случае, когда инвестор не желает получить текущий доход в виде дивидендов. В этом случае доходность (годовая) будет определяться по такой формуле:

,

где

d – прирост курсовой стоимости акций, %;

Р₀ – цена покупки акции, в рублях;

Р₁ – цена продажи акций в рублях;

t – количество дней со дня покупки до дня продажи акции.

2. Облигации.

Рыночная стоимость процентной облигации определяется по такой формуле:

,

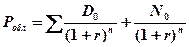где

Р_обл – рыночная стоимость процентной облигации, руб.;

D₀ – сумма процентов по облигации по каждому году, руб.;

N₀ – номинальная стоимость облигации, грн.;

r – средняя ставка доходности на финансовом рынке или дисконтная ставка, доли единицы;

n – число периодов, оставшихся до погашения облигации, лет.

Пример. Определить рыночную стоимость облигации, выпущенную сроком на 7 лет с номинальной стоимостью 1500 руб., купонной ставкой 10 % годовых, оплатой процентов ежегодно, при ставке доходности 15 %.

Р_обл. = 150 / (1+0,15)⁷ + 150 / (1+0,15)⁷ + 150 / (1+0,15)⁷ + 150 / (1+0,15)⁷ + 150 / (1+0,15)⁷ + 150 / (1+0,15)⁷ + 150 / (1+0,15)⁷+ 1500 / (1+0,15)⁷ = 1187,97 руб.

Рыночная стоимость безпроцентной облигации определяется по такой формуле:

.

Для оценки облигаций инвесторы могут использовать такие виды доходности:

1. Купонная доходность (d_k):

,

где

d_K – купонная доходность, %;

D – годовой купонный доход, руб.;

N – номинальная цена (стоимость) облигации, руб.

2. Текущая доходность (d_p):

,

где

d_Р – текущая доходность, %;

PV – цена, по которой была приобретена облигация инвестором, руб.

3. Конечная доходность (d_kon):

,

где

d_kon – конечная доходность, %;

ΔР – прирост или уменьшение капитала, составляющий разницу между ценой реализации (номиналом) и ценой покупки облигации инвестором, руб.;

n – число лет обращения облигации.

4. Для облигаций с нулевым купоном доходность (d) определяется по такой формуле:

,

где

d – доходность облигации;

Р_о – цена покупки облигации, в рублях;

Р_i – цена продажи облигаций, в рублях;

t – количество дней с дня покупки до дня продажи облигации.

5. Расчет ожидаемой прибыльности облигаций (R_o):

.

Пример. Облигация номиналом в 2000 грн. реализуется по цене 1800 руб. Погашение предусматривается через 5 лет. Определите норму ожидаемой прибыльности облигации.

Решение:

или 3,6 %.