
Читайте также:
|
Тема: Вращательное движение твердого тела и его характеристики
Описание вращения точки
Описание вращательного движения тел основывается на описании вращения материальных точек.
Рассмотрим вначале описание вращения единственной материальной точки А. Пусть точка вращается в плоскости X0Y по окружности S относительно центра 0. Радиус окружности r – это модуль радиус-вектора 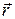 точки А.
Осью вращения является ось Z. Направление вращения показано стрелкой на траектории.
Линейная скорость – это та скорость точки А.
Осью вращения является ось Z. Направление вращения показано стрелкой на траектории.
Линейная скорость – это та скорость  , с которой точка движется вдоль круговой линии; вектор линейной скорости направлен по касательной к траектории.
Пусть в начальный момент точка находилась на оси Х.
Величина, характеризующая изменение положения вращающейся точки, называется вектором угла поворота , с которой точка движется вдоль круговой линии; вектор линейной скорости направлен по касательной к траектории.
Пусть в начальный момент точка находилась на оси Х.
Величина, характеризующая изменение положения вращающейся точки, называется вектором угла поворота  .
За промежуток времени .
За промежуток времени  ее радиус вектор ее радиус вектор 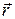 повернется на угол повернется на угол  . Это модуль угла поворота. . Это модуль угла поворота.
| 
|
Сам вектор угла поворота проводят из центра вращения вдоль оси вращения в направлении движения правого винта (направление вращения которого совпадает с направлением вращения точки).
Быстроту вращения характеризуют угловой скоростью. Угловая скорость  – это вектор, лежащий на оси вращения и направленный, как и вектор угла поворота: – это вектор, лежащий на оси вращения и направленный, как и вектор угла поворота:
| 
| ||
«Количество вращательного движения» описывают вектором момента импульса  (см. рис.). (см. рис.).
| |||
| Моментом импульса вращающейся точки называют векторное произведение радиус-вектора и вектора линейной скорости точки: | 
|  Направление момента силы определяется правилом векторного произведения, а также правилом правого винта.
Кратчайшее расстояние от центра вращения до линии действия силы – это плечо силы l.
Направление момента силы определяется правилом векторного произведения, а также правилом правого винта.
Кратчайшее расстояние от центра вращения до линии действия силы – это плечо силы l.
| |
Направление вектора  определяется по правилу векторного произведения. Момент импульса играет ту же роль в описании вращательного движения, что и импульс при описании поступательного движения. определяется по правилу векторного произведения. Момент импульса играет ту же роль в описании вращательного движения, что и импульс при описании поступательного движения.
| |||
| Это хорошо иллюстрирует формула, связывающая момент импульса с угловой скоростью. | 
| ||
| Из нее следует, что вектор момента импульса совпадает по направлению с вектором угловой скорости. | |||
В этой формуле, которая аналогична формуле  , величина J по своей роли аналогична массе. Эта величина характеризует инерционные свойства , величина J по своей роли аналогична массе. Эта величина характеризует инерционные свойства
| |||
| вращающейся материальной точки и называется моментом инерции: | 
| ||
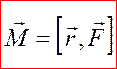
При описании вращения роль силы выполняет момент силы. Моментом силы называют векторное произведение радиус-вектора 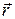 точки приложения силы и вектора силы точки приложения силы и вектора силы  : :
| 
| ||
Следует различать момент силы относительно центра вращения и относительно оси вращения. В общем случае ось вращения может быть ориентирована в пространстве как угодно (не закреплена). В этом случае говорят о моментах (моментах силы, импульса, инерции) относительно точки (центра вращения). Если ось имеет строго определенное положение (закрепленная ось вращения), то говорят о моментах (силы, импульса, инерции) относительно этой оси.
Дата добавления: 2015-02-16; просмотров: 111 | Поможем написать вашу работу | Нарушение авторских прав |