
Читайте также:
|
Система векторов 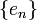 топологического векторного пространства
топологического векторного пространства 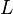 называется базисом Шаудера (в честь Шаудера (англ.)), если каждый элемент
называется базисом Шаудера (в честь Шаудера (англ.)), если каждый элемент  разлагается в единственный, сходящийся к
разлагается в единственный, сходящийся к 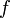 ряд по
ряд по 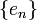 :
:

где  — числа, называемые коэффициентами разложения вектора
— числа, называемые коэффициентами разложения вектора 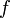 по базису
по базису 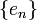 .
.
Чтобы подчеркнуть отличие определения базиса Гамеля для общих линейных пространств (допускаются только конечные суммы) от базиса Шаудера для топологических векторных пространств, для первого часто используют термин линейный базис, оставляя термин базис для разложений в ряды. Мощность линейного базиса называют также линейной размерностью. В конечномерных пространствах эти определения совпадают из-за конечности базиса. В бесконечномерных пространствах эти определения существенно различаются и линейная размерность может быть строго больше мощности базиса Шаудера.
Например, никакое бесконечномерное Гильбертово пространство не имеет счетного линейного базиса, хотя может иметь счетные базисы Шаудера с разложением в ряд, в том числе, ортонормированные базисы. Все ортонормированные базисы Гильбертовых пространств являются базисами Шаудера, например, множество функций 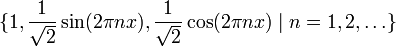 является базисом Шаудера в пространстве
является базисом Шаудера в пространстве 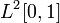 .
.
Дата добавления: 2015-01-30; просмотров: 249 | Поможем написать вашу работу | Нарушение авторских прав |