Прямоугольная декартова система координат

Определение 1. Декартова система координат {0; ; } на плоскости называется прямоугольной, если и - ортогональные единичные векторы.
Аналогично определяется прямоугольная декартова система координат {0; ; ; } в пространстве; в этом случае векторы , , также являются взаимно перпендикулярными и единичными. Базисные векторы , прямоугольной декартовой системы координат на плоскости обозначают обычно , , базисные векторы , , прямоугольной декартовой системы координат обозначают , , . Соответственно разложение радиус-вектора 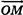по базису записывают в виде

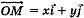(для плоскости);
(для пространства).
В первом случае точка М имеет координаты х, у, во втором случае - координаты х, у, z.

Определение 2. Проекцией вектора на единичный вектор называется число , где = (, ) - угол между векторами и .
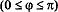Координаты х, у, z вектора , полученные как коэффициенты линейной комбинации базисных векторов, в прямоугольном базисе совпадают с проекцией вектора на базисные орты , , соответственно, а длина вектора равна .