Читайте также:
|
Определение 13.5. Разность между генеральными характеристиками и соответствующими выборочными стати •тиками называется ошибкой выборки, или ошибкой репрезентативности.
Статистические методы позволяют оценить эту разность, которая зависит как от характеристик выборки, так и от ее объема. В процессе выборочного исследования параметры генеральной совокупности определяются в виде интервала, построенного вокруг выборочной статистики. От величины этого интервала и зависит качество исследования.
Из теоремы Чебышева следует, что
(13.2)
Определение 13.6. Таким образом, мы получили интервальную оценку генеральной средней, которая представляет собой доверительный интервал, содержащий оцениваемый параметр генеральной совокупности:
(13.3)
где Δ— предельная ошибка выборки.
Определение 13.7. Интервальной оценкой называют оценку, которая определяется двумя числами — концами интервала, который с определенной вероятностью накрывает неизвестный параметр генеральной совокупности.
Для определения доверительного интервала необходимо вычислить предельную ошибку выборки А, позволяющую установить предельные границы, в которых с заданной вероятностью (надёжностью) должен находиться параметр генеральной совокупности.
Предельная ошибка выборки равна г-кратному числу средних ошибок выборки. Коэффициент t позволяет установить, насколько надежно высказывание о том, что заданный интервал содержит параметр генеральной совокупности.
Если мы выберем коэффициент таким, что высказывание в 97% случаев окажется правильным и только в 3% — неправильным, то мы говорим — со статистической надежностью в 97% доверительный интервал выборочной статистики содержит параметр генеральной совокупности. Статистической надежности в 97% соответствует доверительная вероятность — γ = 0,97.
Если в 5% случаев утверждение «параметр принадлежит доверительному интервалу» будет неверным, то 5% задает уровень значимости — или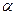 
= 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% ( 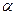< 0,05). Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания. Имеет место соотношение:
(13.4)
Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью, сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала.
(13.5)
где X — средняя по совокупности выбранных единиц;
— средняя по генеральной совокупности;
σген — среднее квадратическое отклонение в генеральной совокупности. Запись показывает, что о величине расхождения между параметром и статистикой 
. можно судить лишь с определенной вероятностью, от которой зависит величина t.
Согласно центральной предельной теореме Ляпунова выборочные распределения статистик (при п 
30) будут иметь нормальное распределение независимо' от того, какое распределение имеет генеральная совокупность. Следовательно имеет место соотношение:
(13.6)
где Ф0(t) — функция Лапласа (см. лекцию 7);
t — аргумент функции Лапласа, зависящий от надежности интервальной оценки;
— средняя по совокупности выбранных единиц;
— средняя по генеральной совокупности;
— ошибка выборки для собственно случайного отбора. Для оценки генеральной доли используется формула:
(13.7)
где со — выборочная доля;
р — генеральная доля;
— доверительная вероятность;
— ошибка выборки для собственно случайного отбора.
Таким образом, для того чтобы найти доверительный интервал для оценки генеральных параметров, достаточно определить величину ошибки. Значения вероятностей, соответствующие различным t, содержатся в специальных
таблицах: при п 30 — в таблице значений Ф0(t) (приложение 2), а при п < 30 в таблице t-распределения Стьюдента (приложение 5). Неизвестное значение σген при расчете ошибки выборки заменяется овы6_.
Средняя ошибка выборки для собственно случайного отбора определяется в зависимости от способа отбора выборки, ошибка выборки определяется по-разному.
Так, для оценки генеральной средней:
► при повторном отборе:
(13-8)
► при бесповторном отборе:
(13.9)
где σ2 — выборочная дисперсия значений признака,
п — объем выборки;
N — объем генеральной совокупности;
— доля обследованной совокупности;
— поправка на конечность совокупности.
Для оценки генеральной доли используются формулы:
► при повторном отборе:
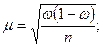
(13.10)
► при бесповторном отборе:
(13.11)
где 
—выборочная дисперсия доли значений признака;
п — объем выборки;
N — объем генеральной совокупности;
— доля обследованной совокупности;
С помощью доверительного интервала можно оценить не только генеральную среднюю, но и другие неизвестные параметры генеральной совокупности.
Для оценки математического ожидания (генеральной средней) нормально распределенного количественного признака Хген по выборочной средней Хвыб при неизвестном среднем квадратическом отклонении σген генеральной совокупности (на практике — при малом объеме выборки, т.е. при п < 30) и собственно-случайном повторном отборе формула интервального оценивания примет вид:
(13.12)
где t определяется по таблицам Стьюдента:
—по уровню значимости α= 1 - γ;
—и числу степеней свободы k =n - 1;
S — исправленное среднее квадратическое отклонение;
п — объем выборки (число обследованных единиц).
Δ определяется по формуле:
(13.13)
Оптимальный объем представительной выборки
В процессе решения задач легко убедиться, что доверительный интервал оценки средней и оценки доли зависит от объема выборки. Чем больше выборка, тем уже будет интервал, тем точнее оценка генеральных статистик. В самом деле, во всех формулах расчета ошибки выборки объем выборки стоит в знаменателе, значит, между объемом выборки и ошибкой существует обратная связь. Самая большая выборка — это вся генеральная совокупность, и тогда оценка вообще будет точечной. При этом, конечно же, не будет соблюдаться экономичность исследования, которая и является целью выборочного метода. Поэтому следует найти такой оптимальный размер выборки, который будет удовлетворять всем требованиям.
Дата добавления: 2015-02-16; просмотров: 139 | Поможем написать вашу работу | Нарушение авторских прав |