Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Линейное распределение электрических зарядов

Вопрос

Электрический диполь – система, состоящая из двух разноименных точечных электрических зарядов, модули которых равны:

-плечо диполя;

O – центр диполя;

Дипольный момент электрического диполя:

, единица измерения - [ 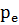]=Кл*м

Реальный пример
электрического диполя

Молекула воды:

Электрическое поле, создаваемое электрическим диполем:
Вдоль оси диполя:

На перпендикуляре к оси диполя:

Картина силовых линий электростатического поля диполя

Силы, действующие на электрический диполь

Однородное электрическое поле:

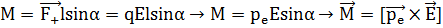
Неоднородное электрическое поле:

Вопрос

Электростатическая
теорема Гаусса

Поток векторного поля

Гидростатическая аналогия:

Для электростатического поля:

Поток вектора напряженности электростатического поля через поверхность пропорционален числу силовых линий, которые пересекают эту поверхность

Дивергенция векторного поля

Определение:

Единицы измерения:

Теорема Остроградского: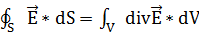

Физический смысл:

расходимость

вектора,

указывает на

наличие источников

поля

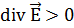
Электростатическая
теорема Гаусса

Заряд внутри замкнутой поверхности:

Поток не зависит от расположения заряда внутри поверхности

Электростатическая
теорема Гаусса

Заряд за пределами замкнутой поверхности:

РИСУНОК!!!

- Поток всегда равен нулю, если заряд вне поверхности

Система заряженных тел:

Ø в соответствии с принципом суперпозиции электростатических полей потоки векторов напряженности полей, создаваемых каждым заряженным телом или частицей в отдельности, следует алгебраически сложить;

Ø при этом следует учесть, что поток создают только те заряженные тела или частицы, которые находятся внутри замкнутой поверхности

Формулировка:

-Поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы пропорционален алгебраической сумме электрических зарядов тел или частиц, которые находятся внутри этой поверхности.

Интегральная форма теоремы:

Интегральная форма записи теоремы для объемного распределения заряда:

Теорема Остроградского:

Дифференциальная (локальная форма записи):

Физическое содержание теоремы:

Ø закон Кулона, поскольку является его прямым математическим следствием;

Ø полевая трактовка закона Кулона на основе концепции близкодействия электростатических взаимодействий;

Ø принцип суперпозиции электростатических полей

Физический смысл теоремы:

Ø дифференциальная форма записи теоремы указывает на заряженные тела и частицы как на источники электростатических полей (положительные электрические заряды как на источники силовых линий поля, а отрицательные – как на стоки силовых линий поля)

7вопрос

Применение электростатической теоремы Гаусса

Различные формы записи теоремы Гаусса:

Для дискретного распределения зарядов:

Для объемного распределения зарядов:

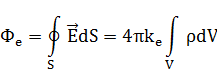
Дифференциальная (локальная форма записи):

Линейное распределение электрических зарядов

Расчет электростатического поля бесконечно длинной тонкой равномерно заряженной нити:

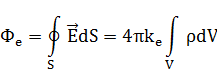
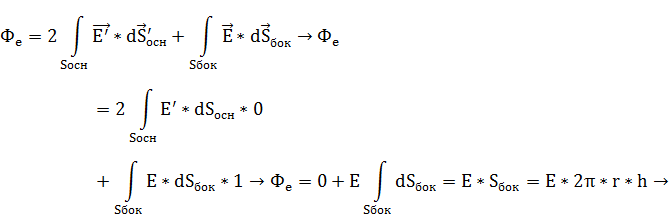
Расчет электростатического поля безграничной равномерно заряженной плоскости:

;

Алгоритм расчета электростатических полей:

Ø из соображений симметрии системы определяем форму силовых линий поля;

Ø выбираем удобную для нахождения потока форму замкнутой поверхности;

Ø находим поток вектора напряженности электростатического поля через эту поверхность;

Ø находим суммарный электрический заряд, который находится внутри этой поверхности;

Ø подставляем полученные значения в теорему Гаусса и находим напряженность поля

8вопрос Потенциал электростатического поля

Потенциал электростатического поля в вакуме

Работа силы:

-криволинейный интеграл.

- циркуль вектора (интегральная хар.)

; ; в-диф=бесконечно малому приращению.

Ротор векторного поля: (локальная характеристика). Разбираем поверхность, ограниченную , на элементарные площадки ;

- циркуляция по контуру ;

- ротор вектора.

Rot векторной величины является вектор. Rot – вихрь.

Циркуляция приходящая на поверхность rot=0 когда проекция =0.

Если работа силы = 0, то и rot=0 и циркуляция.

Теорема Стокса:

циркуляция вектора по замкнутому контуру =потоку. Rot через поверхность ограниченную этим контуром.

циркул=0, то поле без вихревое.

Работа сил электростатического поля.

Силы поля, которое создаёт точечный заряд q перемещает пробный заряд q₀ из точки 1 в точку 2.

Т.о. что работа сил электростатического поля не зависит от формы траекторий по которой заряд перемещается в этом поле, а определяется только положением начальной и конечной точки этого перемещения.

Потенцианальный характер электрического поля.

Поскольку работа силы поля по перемещению в нем подобного электрический заряд не зависит от (перемещения) траектория движения, то электрического поля является потенциальной(безвихревым). Работа силы = 0.

только для поля неподвижного точечного заряда.

Разность потенциалов между 2-мя точками поля.

Разностью потенциалов или напряжением между 2-мя точками электростатического поля наз.отношение работы сил поля по перемещению пробного электрического заряда между данными точками к величине пробного заряда:

Потенциал в данной точке поля:

Если электростатическое поле создало точечным электрическим зарядом q тогда

Потенциалом электростатического поля в точке называется отношение работы сил поля по перемещению пробного электрического заряда из данной точки в к величине этого пробного заряда:

– потенциал поля в точке определен только для поля тех зарядов, которые ограничены в пространстве; если не ограничены, то

Эквипотенциальной поверхностью наз. совокупность точек поля с равным потенциалом.

Они применяют для графика изображения полей.

Вычисление потенциала:

Если электростатическое поле создано точечным электрическим зарядом q, тогда:

В соответствии с принципом суперпозиции электростатического поля потенциалы должны алгебраически суммированы: