Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Кинематика точки

Кинематика Введение в кинематику

Класси́ческая меха́ника — вид механики (раздела физики, изучающего законы изменения положений тел в пространстве со временем и причины, это вызывающие), основанный на законах Ньютона и принципе относительности Галилея.

Пространство. Считается, что движение тел происходит в пространстве, являющимся евклидовым, абсолютным (не зависит от наблюдателя), однородным (две любые точки пространства неотличимы) и изотропным (два любых направления в пространстве неотличимы).

Относительность механического движения: Основным принципом, на котором базируется классическая механика является принцип относительности, сформулированный на основе эмпирических наблюдений Г. Галилеем. Согласно этому принципу существует бесконечно много систем отсчёта, в которых свободное тело покоится или движется с постоянной по модулю и направлению скоростью. Эти системы отсчёта называются инерциальными и движутся друг относительно друга равномерно и прямолинейно. Во всех инерциальных системах отсчёта свойства пространства и времени одинаковы, и все процессы в механических системах подчиняются одинаковым законам. Этот принцип можно также сформулировать как отсутствие абсолютных систем отсчёта, то есть систем отсчёта, каким-либо образом выделенных относительно других

Система отсчёта состоит из тела отсчёта (некоего тела, реального или воображаемого, относительно которого рассматривается движение механической системы), прибора для измерения времени и системы координат.

Кинематика точки

Векторный способ описания движения точки. Положение точки определяется ее радиус-вектором, проведенным из какого-либо центра, который, изменяясь во времени, определяет движение точки, а

- это уравнение движения точки в векторной форме. Траектория движения точки – это непрерывная линия по которой движется точка.

Траектория точки – геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета.

Скорость точки. Скорость точки это вектор, характеризующий изменение положения точки в единицу времени. Вектор скорости определяется по формуле:

При координатном способе описания движения точки вначале определяются проекции скорости на оси координат x, y,z:
, , .

Ускорение точки.

При векторном способе
, [м/сек²].

Проекции ускорения:
. , .

Координатный способ описания движения точки. Положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t).
Если точка движется в плоскости, то уравнений движения два, если по прямой то одно.. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоскости). Если в пространстве, то исключив параметр t, получим два уравнения, которые совместно определяют траекторию движения точки в пространстве.

Естественный способ описания движения точки. Указывается траектория движения точки и закон ее движения по этой траектории, начало и направление отсчета дуговой координаты, а также s=f(t)– закон движения точки.

Про естественный трехгранник в уч. на 110 стр.

Определение ускорения точки по его проекциям на оси естественного трехгранника; касательное и Нормальное ускорения точки: При естественном способе описания движения точки полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения:

.
Модуль нормального ускорения:
,
где r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (^ к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения
,
направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движении направление касательного ускорения и скорости совпадают, при замедленном – противоположно. ^ 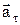, Þ .

Частные случаи движения точки:
1)Прямолинейное: радиус кривизны r= ¥ (бесконечно большой) Þ а_n=0, a=a_t..
2)Равномерное криволинейное движение: v=const Þ a_t=0, a=a_n. Ускорение возникает из-за изменения направления скорости. Закон движения: s=s₀+v×t, при s₀=0, v=s/t.
3)Равномерное прямолинейное движение: а=a_t=a_n=0. Единственное движение, где а=0.
4)Равнопеременное криволинейное движение: a_t=const, v=v₀+a_t×t, . При равноускоренном. движении знаки у a_t и v одинаковы, при равнозамедленном – разные.