Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

РОЗДІЛ 2. Похибки чисельного рішення задачі.

За часи існування ЕОМ найбільш поширеними формами запису чисел у машині були форма запису числа з фіксованою комою та форма запису числа з плаваючою комою.

Фіксована кома:

Усі числа у ЕОМ мають модуль менший за одиницю, а кількість знаків після коми фіксовано. Тоді машина оперує з числами , де q -ціла основа системи числення, a₁,.,a_t цілі у межах від 0 до q.

Плаваюча кома.

Машина оперує з числами де p порядок числа обмежений деякою величиною. На більшості машин ця величина дорівнює 64. Кількість розрядів у числі t може задаватися у деяких випадках користувачем.

Обмеження на представлення числа у ЕОМ може привести до перерви обчислень або до недопустимого погіршення результату за рахунок обчислювальної похибки. Така ситуація можлива у „нестійких” алгоритмах.

Саме побудова „стійких” алгоритмів є задачею теорії чисельних методів.

Похибка при рішенні прикладної задачі обумовлена наступними причинами:

1. Математичний опис прикладної задачі є неточним, неточними є початкові дані

2. Чисельний метод, що застосовується для розв’язку математичної моделі потребує нескінченну кількість кроків у алгоритмі, тому замість точного рішення математичних рівнянь отримують наближені

3. Завдання даних у ЕОМ, виконання арифметичних операцій та виведення результату проводиться з округленням.

Похибки, що виникають з цих причин називаються:

1. похибка, що не ліквідується („спадщина”)

2. похибка методу

3. обчислювальна похибка

Нехай x точне значення параметру, що шукається у прикладній задачі. Тоді є значення того параметру для математичної моделі (точне рішення математичних рівнянь), розв’язок математичних рівнянь за чисельним методом при припущенні, що немає округлення. І, нарешті, наближений розв’язок, що отримуємо при реальних обчисленнях на ЕОМ.

Тоді маємо оцінювати

Якщо x точне значення параметру, що шукається, а x^* відоме наближення до нього, то величину коли

називають абсолютною похибкою, а величину 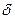коли

називають відносною похибкою.

Для функцій визначається гранична абсолютна та гранична відносна похибказа формулами:

Гранична похибка суми або різниці дорівнює сумі граничних похибок.

Гранична відносна похибка добутку або частки наближено дорівнює сумі граничних відносних похибок.

Значущими цифрами числа називають усі цифри в його запису, починаючи з першої ненульової.

Значущу цифру називають вірною, як що абсолютна похибка числа не перевищує одиниці розряду, що відповідає цій цифрі.

Обмеження на представлення числа у ЕОМ може привести до перерви обчислень або до недопустимого погіршення результату за рахунок обчислювальної похибки. Така ситуація можлива у „нестійких” алгоритмах.

Саме побудова „стійких” алгоритмів є задачею теорії чисельних методів.

При реалізації нестійких алгоритмів навіть коротенька послідовність обчислень може привести до катастрофічної утрати вірних знаків у кінцевому наближеному рішенні.

Як що задача має рішенням величину набагато меншу за нуль, а алгоритм чисельного методу при послідовних обчисленнях має діяти з величинами на декілька порядків більших ніж сам результат, то при великих абсолютних похибках при обчисленні результат отримується без жодного вірного знаку.

Велика абсолютна похибка може бути наслідком відносно невеликої кількості знаків у представленні числа у ЕОМ. Тому такі алгоритми потребують модифікації, щоб послідовність обчислень у ЕОМ була такою, що величини на декілька порядків більше ніж сам результат знаходилися у знаменнику обчислювальних алгоритмів.

Таким чином з’ясовується можлива різниця між формулою методу розв’язку математичної задачі та обчислювальним алгоритмом для реалізації його на конкретній ЕОМ.

Приклад №1. Нехай треба знайти найменший корінь рівняння , якщо розрахунки проводимо у десятковій системі числення та на мантису числа відводиться 4 розряди. (Повинні отримати відповідь y=0.01). Ця відповідь немає жодної значущої цифри.

У прикладі №1 прийшлося віднімати близькі один до одного великі числа, ці числа були округлені з великою абсолютною похибкою. Тут ми вперше зштовхнулися з явищем загубленої значущої цифри. Алгоритм слід так переформулювати, щоб обчислення з великими числами проводились у знаменнику.

Приклад №2. Підрахувати суму 25 членів ряду при умові, що обчислення проводитимуться у десятковій системі з п’ятьма знаками у представленні числа для значення x=-5.5 (Порівняти свою відповідь з зразковою відповіддю 0,0026363.

Так у прикладі №2 деякі члени суми, а саме п’ятий, мають похибку округлення май же рівну самому кінцевому результату. На представлення перших десяти членів ряду витрачено два знаки до десятинної коми і лишилось три знаки після десятинної коми. В той час як у остаточному результаті значущі цифри починаються з третього знаку після коми. Такий алгоритм потребує модифікації так, щоб великі члени суми знаходилися у знаменнику формули алгоритму.

Деякі задачі дуже чуткі до невеликої зміни початкових даних. Ці факти вже не залежать від плаваючої системи або обраного алгоритму. Тому подолати проблеми похибок у таких задачах модифікацією алгоритму вже не можна. Для них треба використовувати спеціальні методи та прийоми зміни самих рівнянь для покращення їх обчислювальних властивостей. Прикладом такої модифікації може бути масштабування рівнянь, тобто помноження одного з рівнянь системи на масштабуючий коефіцієнт з метою деякого зрівняння до однаких порядків усіх коефіцієнтів системи.