Читайте также:
|
Рангом матрицы A максимальное количество линейно независимых строк матрицы A. (или это количество базисных строк)
Теорема о базисном миноре. Следствие.
Любая строка матрицы A линейно выражается через базисные строки матрицы A.
Доказательство:
Пусть 
– строки матрицы A.
Пусть 
Пусть строка 
, тогда система строк 
- линейно зависима => 
,
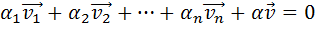ч.т.д.
Следствие:
Если |A|=0 и r(A)<n, то строки и столбцы матрицы A линейно зависимы.
Элементарные преобразования матрицы, не изменяющие ранг.
1.) Любые 2 строки матрицы можно поменять местами.
2.) Любую строку матрицы можно умножить на отличное от нуля число.
3.) Нулевую строку матрицы можно вычеркнуть.
4.) К любой строке можно прибавить любую другую строку, умноженную на любое число.
5.) 1-4 пункты справедливы и для столбцов матрицы.
Дата добавления: 2015-02-16; просмотров: 68 | Поможем написать вашу работу | Нарушение авторских прав |