Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Достаточное условие сходимости метода простых итераций при решении трансцендентных уравнений

Пусть выполнены условия:

1. Нелинейное уравнение имеет решение .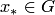

2. Отображение 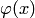является сжимающим в области с некоторым коэффициентом .

Тогда:
а) решение 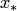является единственным решением в области ;

б) последовательность , определяемая по отображению на основе итерационного процесса, сходится к решению 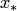со скоростью геометрической прогрессии;

Теорема 3.9 утверждает, что при выполнении условий 1,2 существует окрестность 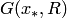такая, что если взять 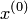в этой окрестности и вычислять 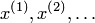по формуле (3.9), то в результате с любой наперед заданной точностью можно вычислить 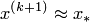, соответствующее искомому (единственному) корню. Но так как эта окрестность неизвестна, то можно взять произвольное 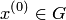. Если при этом вычисляется последовательность 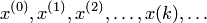, сходящаяся к некоторому значению , то в силу теоремы . 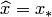Если сходимость отсутствует, то надо взять другое 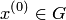и повторить расчет.