Читайте также:
|
1. Частота появления события А в опытах равна: отношению числа опытов, в которых произошло событие А, к n.
2. Выборка объёмом n будет репрезентативной (представительной), если: её осуществлять случайно.
3. Проверка гипотезы о том, что случайные величины Х и Y имеют одинаковый закон распределения выполняются с помощью: критерия Уилкоксона.
4. Проверка гипотезы о равенстве дисперсий случайных величин X и Y выполняется с помощью: F – критерия.
5. Проверка гипотезы о равенстве математических ожиданий случайных величин X и Y выполняется с помощью: i - критерия.
6. Оценка Q* называется эффективной, если её дисперсия минимальна по отношению к дисперсии любой другой оценки этого параметра.
7. Оценка Q* называется состоятельной, если при увеличении объёма выборки n она сходится по вероятности к значению параметра Q.
8. Оценка Q* называется несмещённой, если её математическое ожидание точно равно параметру Q для любого объёма выборки.
9. Ошибка первого рода (“ пропуск цели”) для двух альтернативной гипотезы {Н0.Н1} состоит в том, что: будет отклонена гипотеза Н0, если она верна.
10. Ошибка второго рода (“ложное срабатывание”) для двух альтернативной гипотезы {Н0.Н1} состоит в том, что: будет принята гипотеза Н0 если она верна.
11. Прямоугольники равновероятностной гистограммы имеют одинаковую: площадь.
12. Корреляционное поле (диаграмма рассеивания) для двумерной случайной величины (X,Y), это: изображение в виде точек на плоскости в декартовой системе координат результатов опыта.
13. Уровень значимости это: вероятность совершить ошибку первого рода.
14. Самостоятельная несмещённая оценка дисперсии равна: 
15. Проверка гипотезы об отсутствии корреляционной зависимости для двумерной случайной величины (X,Y), распределённой по нормальному закону, по выборке объёмом n=25 выполняется с помощью критерия: 
16. Проверка гипотезы об отсутствии корреляционной зависимости для двумерной случайной величины (X,Y), распределённой по нормальному закону, по выборке объёмом n=100 выполняется с помощью критерия:: 
17. Доверительный интервал для математического ожидания случайной величины Х с неизвестным законом распределения имеет вид: 
18. Доверительный интервал для дисперсии случайной величины Х с неизвестным законом распределения имеет вид: 
19. Система уравнений в методе наименьших квадратов для сглаживания кривой 
имеет вид: 
20. Критерий Колмогорова имеет вид: 
21. Целевая функция метода наименьших квадратов имеет вид: 
22. Последовательность случайных величин Хn сходится по вероятности к величине а, 
, если дляe, d - произвольных сколь угодно малых положительных чисел: p(|X – mx|<e)>1-d
23. Состоятельная оценка математического ожидания равна: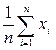 
24. Состоятельная оценка коэффициента корреляции вычисляется по формуле: 
25. Величина Х в 10 опытах приняла значения 4, 1, 3, 4, 2, 5, 1, 3, 6, 4. Эмпирическая функция распределения F*(3) равна: 0.3
26. Величина Х в 10 опытах приняла значения 4, 1, 3, 4, 2, 5, 1, 3, 6, 4. Эмпирическая функция распределения F*(1) равна: 0
27. Величина Х в 10 опытах приняла значения 4, 1, 3, 4, 2, 5, 1, 3, 6, 4. Оценка вероятности того, что Х = 4 равна: 0.3
28. Величина Х в 10 опытах приняла значения 4, 1, 3, 4, 2, 5, 1, 3, 6, 4. Вариационный ряд будет иметь вид: 1, 1, 2, 3, 3, 4, 4, 4, 5, 6.
29. Объём выборки равен 80. Число интервалов в интервальном статистическом ряде следует взять равным: 9.
30. Объём выборки равен 10000. Число интервалов в интервальном статистическом ряде следует взять равным: 15.
31. По выборе объёмом 100 значений случайной величины Х построен интервальный статистический ряд, содержащий 10 интервалов, и выдвинута гипотеза о нормальном законе распределения случайной величины Х. Число степеней свободы для критерия Пирсона равно: 7.
32. По выборе объёмом 100 значений случайной величины Х построен интервальный статистический ряд, содержащий 10 интервалов, и выдвинута гипотеза о экспоненциальном законе распределения случайной величины Х. Число степеней свободы для критерия Пирсона равно: 8.
33. В первой серии из 25 опытов событие А появилось в 5 опытах, во второй серии из 100 опытов событие А появилось в 25 опытах. Критерий для проверки гипотезы о равенстве вероятностей события А в этих сериях равен: 1/20.
Дата добавления: 2015-02-16; просмотров: 107 | Поможем написать вашу работу | Нарушение авторских прав |