
Читайте также:
|
1. Случайная величина Х с нормальным законом распределения принимает значения [ -∞:+∞]
2.случайная величина Х с экспоненциальным законом распределения принимает значения [0:+∞].
3. функцией распределения F(x) случайной величины Х называется вероятность того что: она примет значение меньшее чем аргумент функции.
4. математическое ожидание дискретной случайной величины Х равно: 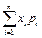
5. дисперсия случайной величины Х характеризует: степень рассеивания значений случайной величины
6. дисперсия суммы случайных величин Х и Y равна: Dx+Dy+2Kxy
7. дисперсия случайной величины Х равна: µ2(х)
8. Мода случайной величины Х равна: наиболее вероятному значению случайной величины.
9.функция распределения F(x) является: неубывающей функцией.
10. для функции распределения F(x) имеет место предельное соотношение: F(+∞)=1
11. для функции распределения F(x) имеет место предельное соотношение: F(-∞)=1
12. математическое ожидание центрированной случайной величины Х равно: 0
13. практически все значения случайной величины Х находятся в интервале: [mx-3σx; mx+3σx]
14.вероятность попадания случайной величины Х в интервал [a;b) равна: 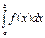
15. математическое ожидание индикатора случайного события A(p(A)=p) равно: p
16. дисперсия индикатора случайного события A(p(A)=p) равно:  pq
pq
17. дискретная случайная величина Х имеет геометрическое распределение, если она принимает значения 0,1,…. с вероятностями: p(X=i)=qip
18. дискретная случайная величина Х имеет распределение Пуассона, если она принимает значения 0,1,…. с вероятностями: p(X=i)= 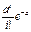
19. интервал времени между двумя соседними событиями простейшего потока случайных событий имеет распределение: экспоненциальное
20. медиана случайной величины Х равна: значению для которого выполняется условие p{X<M0}= p{X>M0}=0.5
21.для независимых случайных величииХ1,Х2,…,Хn корреляционная матрица имеет вид: все элементы кроме диагональных равны 0
22.характеристическая функция случайной величины Х равна: υx(t)=M(eitx)
23.плотность распределения f(x) равна: 
24. плотность распределения f(x) принимает значения: [0;+∞]
25.переход от плотности распределения f(x) к функции распределения F(x) имеет вид: 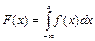
26.число событий простейшего потока событий, поступивших в течении некоторогоинтервала,имеет распределение: Пуассона
27. M[X]=1 математическое ожидание величины Y=4-2X равно: 2
28. D[X]=1 дисперсия величины Y=4-2X равно: 4
29.случайная величина Х распределена равномерно на интервале [-1;1]. Y=x2. Математическое ожидание величины Y равно: 1/3
30.дисперсия случайной величины, равномерно распределённой в интервале [1;5] равна: 4/3
31.функция распределения случайной величины Y=u(x), где u(x)- монотонно возрастающая функция, вычисляется по формуле: 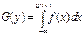
32.функция распределения случайной величины Y=u(x), где u(x)- монотонно убывающая функция, вычисляется по формуле: 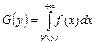
33.плотность распределения случайной величины Y=u(x), где u(x)- монотонно убывающая функция, вычисляется по формуле: 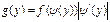
34.плотность распределения случайной величины Y=u(x), где u(x)- монотонно возрастающая функция, вычисляется по формуле: 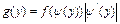
35.нормальной случайной величины Х с математическим ожиданием M[X]=2 и дисперсией D[X]=9 медиана равна: 2
36.математическое ожидание случайной величины, равномерно распределённой в интервале [1;5] равно: 3
37.условие нормировки имеет вид:
38.случайная величина Х распределена равномерно на интервале [-1;4]. Y=|x|. Плотность вероятности величины Y равна: 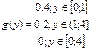
Дата добавления: 2015-02-16; просмотров: 198 | Поможем написать вашу работу | Нарушение авторских прав |