Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Закон сохранения импульса. Реактивное движение.

Пусть на тело массой m в течение некоторого малого промежутка времени действовала сила. Под действием этой силы скорость тела изменилась на некоторую величину. Следовательно, в течение этого времени тело двигалось с ускорением.

Из основного закона динамики (второго закона Ньютона) следует: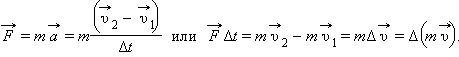

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).

Физическая величина, равная произведению силы на время ее действия, называется импульсом силы. Импульс силы также является векторной величиной.

Второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.

Обозначив импульс тела буквой p второй закон Ньютона можно записать в виде

Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу.

Если движение тела во время действия силы происходило по некоторой криволинейной траектории, то начальный и конечный импульсы тела могут отличаться не только по модулю, но и по направлению. В этом случае для определения изменения импульса удобно использовать диаграмму импульсов, на которой изображаются вектора начального и конечного импульса, а также вектор изменения импульса, построенный по правилу параллелограмма. В качестве примера на рис. изображена диаграмма импульсов для мяча, о тскакивающего от шероховатой стенки. Мяч массой m налетел на стенку со скоростью под углом α к нормали (ось OX) и отскочил от нее со скоростью под углом β. Во время контакта со стеной на мяч действовала некоторая сила F, направление которой совпадает с направлением вектора .

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.

Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим:

По третьему закону Ньютона

Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны:

Применим к этим телам второй закон Ньютона:

где и – импульсы тел в начальный момент времени, и – импульсы тел в конце взаимодействия. Из этих соотношений следует: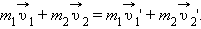

Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.

Рис. иллюстрирует закон сохранения импульса на примере нецентрального соударения двух шаров разных масс, один из которых до соударения находился в состоянии покоя.

Изображенные на рис. вектора импульсов шаров до и после соударения можно спроектировать на координатные оси OX и OY. Закон сохранения импульса выполняется и для проекций векторов на каждую ось.

^ Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.

При стрельбе из орудия возникает отдача – снаряд движется вперед, а орудие – откатывается назад. Снаряд и орудие – два взаимодействующих тела. Скорость, которую приобретает орудие при отдаче, зависит только от скорости снаряда и отношения масс. Если скорости орудия и снаряда обозначить через и а их массы через М и m, то на основании закона сохранения импульса можно записать в проекциях на ось OX

На принципе отдачи основано реактивное движение. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью u относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. Тогда для замкнутой системы «ракета + газы» можно записать на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия):

где V – скорость ракеты после истечения газов.

Здесь предполагалось, что начальная скорость ракеты равнялась нулю.

Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.

Вопрос 12

Закон движения центра масс.

Воспользовавшись законом изменения импульса, получим закон движения центра масс:

d P /dt = M∙d V _c/dt = Σ F _i

Центр масс системы движется так же, как двигалась бы частица с массой, равной массе системы, под действием силы, равной векторной сумме всех внешних сил, действующих на входящие в систему частицы.

В частности, центр масс замкнутой системы относительно произвольной ИСО движется равномерно прямолинейно или покоится. Изменение импульса центра масс происходит за счет внешних сил.

Внутренние силы не влияют на характер его движения, если внешнее воздействие на систему постоянно и однородно. Например, во время салюта движение центра масс разорвавшегося пиротехнического снаряда в постоянном однородном поле силы тяжести происходит по параболе.

Если внешнее воздействие изменяется, то на различные части системы начинают действовать разные силы и характер движения центра масс меняется. В качестве примера рассмотрим движение системы, состоящей из одного тела - снаряда. В случае падения одной из частей разорвавшегося в воздухе снаряда на землю в системе появится новая внешняя сила - сила реакции опоры. Характер движения центра масс системы (осколков снаряда) при этом изменится. Наличие внутренних сил в этом примере является необходимым условием изменения характера движения центра масс системы. Без этих сил, обусловивших распад снаряда на части, не произошло бы изменения траектории его движения вплоть до падения снаряда на землю.

Энергия – универсальная мера различных форм движения и взаимодейст-

вия. С различными формами движения материи связаны различные формы энер-

гии: механическая, тепловая, электромагнитная, ядерная и др. В одних явлениях

форма движения материи не изменяется (например, горячее тело нагревает хо-

лодное), в других – переходит в иную форму (например, в результате трения ме-

ханическое движение превращается в тепловое). Однако существенно, что во всех

случаях энергия, отданная (в той или иной форме) одним телом другому телу,

равна энергии, полученной последним телом.

Изменение механического движения тела вызывается силами, действующи-

ми на тело со стороны других тел. Чтобы количественно характеризовать процесс

обмена энергией между взаимодействующими телами, в механике вводится поня-

тие работы силы.

Если тело движется прямолинейно и на него действует постоянная сила F

r

,

которая составляет некоторый угол a с направлением перемещения s

r

, то работа

этой силы равна скалярному произведению векторов F

r

и s

r

или произведению

проекции силы s F на направление вектора перемещения (F = Fs cosa) s, умно-

женной на перемещение точки приложения силы

A = Fs = F s = Fs cosa s

rr

. (9.1)

В общем случае сила может изменяться как по модулю, так и по направле-

нию, поэтому формулой (9.1) пользоваться нельзя. Если, однако, рассмотреть эле-

ментарное перемещение dr

r

, то силу F

r

можно считать постоянной, а движение

точки ее приложения – прямолинейным.

Элементарной работой силы F

r

на перемещение dr

r

называется скалярная вели-

чина

dA Fdr F ds F ds

s = = cosa =

r r

,

где a – угол между векторами F

r

и dr

r

; ds dr

r = –

элементарный путь; s F – проекция вектора F

r

на

вектор dr

r

(рис. 13).

Работа силы на участке траектории от точки 1 до точки 2 равна алгебраиче-

ской сумме элементарных работ на отдельных бесконечно малых участках пути.

Эта сумма приведена к интегралу

= ∫ a = ∫

A Fds cos F ds s. (9.2)

Для вычисления этого интеграла надо знать

зависимость силы s F от пути s вдоль траектории 1–2.

Пусть эта зависимость представлена графически (рис.

14), тогда искомая работа A определяется на графике

площадью заштрихованной фигуры. Если, например,

тело движется прямолинейно, сила F = const и

a = const, то получим

= ∫ cosa = cosa∫ = cosa

A Fds F ds Fs,

где s – пройденный телом путь.

Из формулы (9.1) следует, что при a < p 2 A > 0, в этом случае состав-

ляющая s F совпадает по направлению с вектором скорости v

r

(рис.13). Если

a > p 2, то A < 0. При a = p 2 A = 0.

[ A ] = [Дж] = [Н×м]

Чтобы охарактеризовать скорость совершения работы, вводят понятие