Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Решение НУ. Метод итераций

Обоснование

Чтобы численно решить уравнение 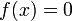методом простой итерации, его необходимо привести к следующей форме: , где — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения должно выполняться условие . Решение данного уравнения ищут в виде , тогда:

В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

С учётом этого функция определяется выражением:

Эта функция в окрестности корня осуществляет сжимающее отображение^[1], и алгоритм нахождения численного решения уравнения 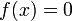сводится к итерационной процедуре вычисления:

По теореме Банаха последовательность приближений стремится к корню уравнения .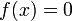

Иллюстрация метода Ньютона (синим изображена функция 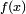, нуль которой необходимо найти, красным — касательная в точке очередного приближения ). Здесь мы можем увидеть, что последующее приближение 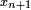лучше предыдущего .

Геометрическая интерпретация

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть — определённая на отрезке и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где α — угол наклона касательной в точке .

Следовательно искомое выражение для 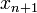имеет вид:

Итерационный процесс начинается с некоего начального приближения x ₀ (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).

[править] Алгоритм

Задается начальное приближение x ₀.

Пока не выполнено условие остановки, в качестве которого можно взять или (то есть погрешность в нужных пределах), вычисляют новое приближение: .

6.Метод Гаусса. Классическим методом решения систем линейных алгебраических уравнений является метод последовательного исключения неизвестных – метод Гаусса (его еще называют методом гауссовых исключений). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

Процесс решения по методу Гаусса состоит из двух этапов: прямой и обратный ходы.

В данном разделе на трех различных примерах покажем, какметодом Гаусса можно решить СЛАУ.

Пример 1. Решить СЛАУ 3-го порядка.

Обнулим коэффициенты при во второй и третьей строчках. Для этого домножим их на 2/3 и 1 соответственно и сложим с первой строкой:

Теперь обнулим коэффициент при в третьей строке, домножив вторую строку на 6 и вычитая из неё третью:

В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.

На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:

из третьего;

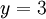из второго, подставив полученное ;

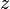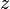из первого, подставив полученные и .

В случае, если число уравнений в совместной системеполучилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.